There is something wrong with this example from New Senior Mathematics Advanced on pages 561-562. Can you see what it is?
(Hint 1: there is nothing wrong with the calculation.)
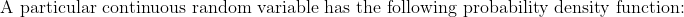
 = \begin{cases}-3(x-1)^2+2,&0\le x\le1 \\0,&\text{otherwise}\end{cases})
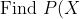\le0.7.)
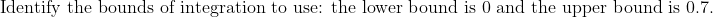
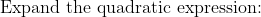
^2+2&=-3(x^2-2x+1)+2\\&=-3x^2+6x-3+2\\&=-3x^2+6x-1\end{aligned})
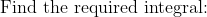
\ dx&=[-x^3+3x^2-x]_0^{0.7}\\&=(-(0.7)^3+3\times(0.7)^2-0.7)-0\\&=0.427\end{aligned})
(Hint 2: you can fix it by replacing -3(x-1)2+2 with -6(x-0.5)2+1.5 in which case the answer is 0.784 - but can you see why?)
(Hint 3: without changing the function find P(X ≤ 0.1) instead.)
(Hint 1: there is nothing wrong with the calculation.)
(Hint 2: you can fix it by replacing -3(x-1)2+2 with -6(x-0.5)2+1.5 in which case the answer is 0.784 - but can you see why?)
(Hint 3: without changing the function find P(X ≤ 0.1) instead.)
Last edited:
