Yes, a hint would help. I truly am stumped by this questionAny hint?
-
Looking for HSC notes and resources? Check out our Notes & Resources page
MX2 Integration Marathon (1 Viewer)
- Thread starter dan964
- Start date
Paradoxica
-insert title here-
I don't believe it has a solution contained within MX2. But feel free to take that as a challenge.
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
I'm really lost. I tried to express the integral in various alternative ways but I can't solve any of these.
Have you tried writing the last one in terms of the hyperbolic functions?I'm really lost. I tried to express the integral in various alternative ways but I can't solve any of these.
dx)
That's an excellent variety of integrals, none of which are on the right track (from what I've explored at least). My method is not that nice but it does yield a solution. My first hint is to tryI'm really lost. I tried to express the integral in various alternative ways but I can't solve any of these.
dx)
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
Many alternative forms that lead me to nowhere
Why is pi^2/8 appearing so often?
}dx)
}dx)
}dx)
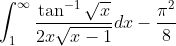
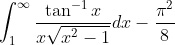
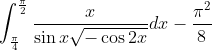
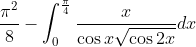
Why is pi^2/8 appearing so often?
That's what I like about this question - due to the simplicity of the q, there seem to be so many ways of approaching it which don't go anywhereMany alternative forms that lead me to nowhere
Why is pi^2/8 appearing so often?
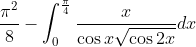
Paradoxica
-insert title here-
^I don't believe it has a solution contained within MX2. But feel free to take that as a challenge.
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
Please correct me if there is any typo.Another problem if u get bored of that one:
No using dilogarithms, only 4U stuff.
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
Do you have more hints?That's what I like about this question - due to the simplicity of the q, there seem to be so many ways of approaching it which don't go anywhere
I mean, you have to show why that sum isPlease correct me if there is any typo.
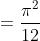
After a partial evaluation of the integral, you should get the original integral, which you can use for symmetry. See how that's possible. (note that this is quite cancerous to do, so you need to have some persistence)Do you have more hints?
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
A few more alternative expressions that look interesting but not leading to a solution
dx)
dx)
dx)
dx)
dx)
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
Some more interesting expressions but no success
dx)
dx)
dx)
dx)
@sharky564 I wanna give up. How did you solve this integral?
@sharky564 I wanna give up. How did you solve this integral?
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
I have decided to give up @sharky564 question.
This is a new question that should be solvable in 4U.
^{\pi-1}+\left(1-\sin\sqrt{x}\right)^{\pi-1}}{\left(1+\sin\sqrt{x}\right)^{\pi}+\left(1-\sin\sqrt{x}\right)^{\pi}}dx$.)
This is a new question that should be solvable in 4U.
Last edited:
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
One more question
^{n}+\left(1-\sin\sqrt{x}\right)^{n}}{\left(1+\sin\sqrt{x}\right)^{n+1}+\left(1-\sin\sqrt{x}\right)^{n+1}}dx)
(It can be solved without knowing the result in #217. )
)
(It can be solved without knowing the result in #217.
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
This question can take ages if you're not on the right track.
^{m}x^{n}dx}{\int_{0}^{1}\log_{2}\left(\sqrt[n+1]{\frac{\left(16^{\sqrt{x}}+k\cdot4^{\sqrt{x}}+4\right)\left(16^{1-\sqrt{x}}+k\cdot4^{1-\sqrt{x}}+4\right)\left(\sec^{2}\frac{\pi x}{4}+2\tan\frac{\pi x}{4}\right)^{a}}{\left(4^{\sqrt{x}}+k\cdot2^{\sqrt{x}}+4\right)\left(4^{1-\sqrt{x}}+k\cdot2^{1-\sqrt{x}}+4\right)\left(\sin\frac{\pi x}{2}\right)^{b}\left(\cos\frac{\pi x}{2}\right)^{c}}}\right)dx}=\left(1+a+b+c\right)^{m-1})
(modified to make it look more evil ...feel free to share your attempt)
...feel free to share your attempt)
(modified to make it look more evil
Last edited:
