Isn't that just a u sub. Let u = tanxint(e^tanx)/cos^2(x)
-
Looking for HSC notes and resources? Check out our Notes & Resources page
MX2 Integration Marathon (2 Viewers)
- Thread starter dan964
- Start date
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
It is very quiet recently.
Feel free to share your attempt.
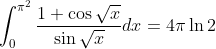
Feel free to share your attempt.
Not sure if this method is any good...
Attachments
-
283.5 KB Views: 51
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
This one should be harder.
I think I've masked the underlying substitution quite well.
\tan x}\right)}{\sin^{2}\left(\frac{\pi}{3}-x\right)+\cos^{2}x}dx)
I think I've masked the underlying substitution quite well.
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
Anyone has guessed the substitution?This one should be harder.
I think I've masked the underlying substitution quite well.
\tan x}\right)}{\sin^{2}\left(\frac{\pi}{3}-x\right)+\cos^{2}x}dx)
Paradoxica
-insert title here-
I can reduce it but I can't evaluate it. Are you sure this integral is expressible in terms of elementary functions?Anyone has guessed the substitution?
The numerical integration returns 0.4690815321272337326612091235046416327076, which has no simple form in the Inverse Symbolic Calculator.
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
I think you ignored the base of the log and got (pi/12) ln 6.
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
Once the substitution is uncovered, it is not much fun.
\right))
}{1+\left(\sqrt{3}-2\tan\left(x-\frac{\pi}{6}\right)\right)^{2}}=\frac{-\frac{1}{2}}{\sin^{2}\left(\frac{\pi}{3}-x\right)+\cos^{2}x})
Paradoxica
-insert title here-
tried this as my initial thought (i knew getting rid of the denominator was a necessary step), didn't get very far for some reason, maybe i made an arithmetical error somewhereOnce the substitution is uncovered, it is not much fun.
pikachu975
Premium Member
Damn this thread is still going... throwbacks
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
This one should be easier.
dx)
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
a new one...shouldn't be too hard
Feel free to share your attempt.
Find the area bounded by x-axis and the curve
\left(1+\pi^{x}\right)}) .
.
Feel free to share your attempt.
Find the area bounded by x-axis and the curve
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
This one should be easier.
dx)
Not sure if this is still active but I'll give this a go for fun (let me know if I've made any mistakes or there is an easier way). The x-ints area new one...shouldn't be too hard
Feel free to share your attempt.
Find the area bounded by x-axis and the curve
.
Using the corrected identity (Thanks to vernburn for showing that there is a factor of a half):
where E is an even function and O is an odd function. The integral simplifies:
Let
So
Last edited:
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
Your approach is correct but unfortunately a factor of 1/2 is missing somewhere.
\left(1+\pi^{x}\right)}dx=\frac{\pi}{48}-\frac{\sqrt{3}}{32}\pi+\frac{1}{8})
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
another one
Feel free to share your attempt.
\cos\left(x^{x}-\ln x\right)\log_{2}\left(ex\right)dx=\frac{\left(5\ln2-8\right)\sin\left(2\ln2\right)+\left(4-5\ln2\right)\sin\left(4\ln2\right)+\left(10\ln2-6\right)\cos\left(2\ln2\right)+\left(3-10\ln2\right)\cos\left(4\ln2\right)}{100\ln2})
Feel free to share your attempt.
Not quite sure where I missed the half, but I might not have checked it properly.Your approach is correct but unfortunately a factor of 1/2 is missing somewhere.
\left(1+\pi^{x}\right)}dx=\frac{\pi}{48}-\frac{\sqrt{3}}{32}\pi+\frac{1}{8})
I believe the factor of a half comes from the identity you (incorrectly) quoted. The identity should be:Not quite sure where I missed the half, but I might not have checked it properly.
Proof:
Using the identity:another one
Feel free to share your attempt.
\cos\left(x^{x}-\ln x\right)\log_{2}\left(ex\right)dx=\frac{\left(5\ln2-8\right)\sin\left(2\ln2\right)+\left(4-5\ln2\right)\sin\left(4\ln2\right)+\left(10\ln2-6\right)\cos\left(2\ln2\right)+\left(3-10\ln2\right)\cos\left(4\ln2\right)}{100\ln2})
For the second integral, let
Now for the first integral letting
So in total:
Wow that was a long one, unfortunately didn't get it out as I'm off by a bit, can anyone see my error?
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
This is the product of two functions. You cannot substitute and multiply this way.
Wow that was a long one, unfortunately didn't get it out as I'm off by a bit, can anyone see my error?

