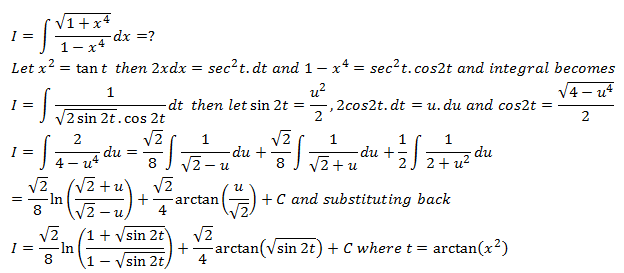stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
Re: HSC 2018 MX2 Integration Marathon
If you are careful with the manipulation, you should have got the final answer.
(x^2-2x+2)}}{(x^2-4x+2)(x^2-4x+6)(4+2^x)}dx)
^4+4}}{\left(\left(x-2\right)^4-4\right)(1+2^{x-2})}dx)
(1+2^y)}dy)
}dy)
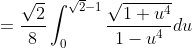
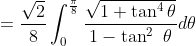
}{\sqrt{2-\sin^2 (2\theta)}}d\theta+\frac{1}{8}\int_0^{\frac{\pi}{8}}\frac{\sec^2 (2\theta)}{\sqrt{2+\tan^2 (2\theta)}}d\theta)
+\frac{1}{16}\ln\left(\tan2\theta+\sqrt{2+\tan^2 2\theta}\right)\right]_0^{\frac{\pi}{8}})
 + \frac{\ln\left(1+\sqrt{3}\right)}{16}-\frac{\ln\sqrt{2}}{16})
}{16}-\frac{\ln2}{32})
Not sure if anyone attempted to go further from this.This is a skeleton solution.
By substituting u=(x-2)/sqrt(2) and considering f(x)+f(-x), the integral can be re-written as
A tangent substitution will turn it into a format that Wolfram can solve...finally
https://www.wolframalpha.com/input/?i=integrate+sqrt(1+tan^4+x)+/+(1-tan^2+x)
I know Wolfram used hyperbolic tangent substitution but it is also solvable in MX2 by secant substitution.
Alternatively, if you don't mind handling improper integral, you can do some algebraic manipulation to get:
Substituting v=u-1+u and w=u-1-u will lead to two improper (but solvable) integrals because u-1 blows up at 0.
If you are careful with the manipulation, you should have got the final answer.