-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
HSC 2014 MX2 Marathon ADVANCED (archive) (4 Viewers)
- Thread starter Trebla
- Start date
- Status
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
}=(2^b-1)\sum_{j=1}^k 2^{b(j-1)}.)
I've finished MX2 now, but this thread is too fun lol.
Axio
=o
- Joined
- Mar 20, 2014
- Messages
- 484
- Gender
- Male
- HSC
- 2015
Re: HSC 2014 4U Marathon - Advanced Level
Can I ask how you know to turn that statement into that sum?I've finished MX2 now, but this thread is too fun lol.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
RealiseNothing
what is that?It is Cowpea
Re: HSC 2014 4U Marathon - Advanced Level
Prove that the tangents are opposite vertices of a cyclic quadrilateral intersect on the secant through the other two verticies IF AND ONLY IF the two products of opposite sides of the cyclic quadrilateral are equal (so prove both ways)
Prove that the tangents are opposite vertices of a cyclic quadrilateral intersect on the secant through the other two verticies IF AND ONLY IF the two products of opposite sides of the cyclic quadrilateral are equal (so prove both ways)
Axio
=o
- Joined
- Mar 20, 2014
- Messages
- 484
- Gender
- Male
- HSC
- 2015
Re: HSC 2014 4U Marathon - Advanced Level
Let A, B, C and D be the sides of a cyclic quadrilateral and E be an external point and let two equal tangents from the external point E meet the circle at A and C.
Any secant that passes through E, B and D is a diagonal to the cyclic quadrilateral ABCD.
Hence AB/AD=BC/DC, making (AB)(DC)=(AD)(BC).
Going backwards: assume (AB)(DC)=/=(AD)(BC).
Therefore triangles are not similar (unless (AB)(BC)=(AD)(DC)).
Therefore ABCD is not a cyclic quadrilateral, which is a contradiction.
Does this work?
Let A, B, C and D be the sides of a cyclic quadrilateral and E be an external point and let two equal tangents from the external point E meet the circle at A and C.
Any secant that passes through E, B and D is a diagonal to the cyclic quadrilateral ABCD.
Hence AB/AD=BC/DC, making (AB)(DC)=(AD)(BC).
Going backwards: assume (AB)(DC)=/=(AD)(BC).
Therefore triangles are not similar (unless (AB)(BC)=(AD)(DC)).
Therefore ABCD is not a cyclic quadrilateral, which is a contradiction.
Last edited:
Re: HSC 2014 4U Marathon - Advanced Level
secondly, I think you're making wrong assumptions, for example opposite triangles in cyclic quads aren't necessarily similar.
in other words, you've only proven it only one way.
For backwards, you're supposed to explicitly prove that if (AB)(DC)=(AD)(BC), then the inteserction of the tangents at A and C go through the secant of B and D, which you've NOT done. What you've proven is that if tangents at A and C go through secant of B and D, then (AB)(DC)=(AD)(BC)
So your answer is incomplete. You didn't even do the hard bit lol
firstly, i don't think you know what if and only if means.
secondly, I think you're making wrong assumptions, for example opposite triangles in cyclic quads aren't necessarily similar.
in other words, you've only proven it only one way.
For backwards, you're supposed to explicitly prove that if (AB)(DC)=(AD)(BC), then the inteserction of the tangents at A and C go through the secant of B and D, which you've NOT done. What you've proven is that if tangents at A and C go through secant of B and D, then (AB)(DC)=(AD)(BC)
So your answer is incomplete. You didn't even do the hard bit lol
Axio
=o
- Joined
- Mar 20, 2014
- Messages
- 484
- Gender
- Male
- HSC
- 2015
Re: HSC 2014 4U Marathon - Advanced Level
Lol I just realised what I was doing wrong with the similar triangles :S...
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
So let ABCD be the cyclic quad in anticlockwise order, and we are drawing tangents at A and C.
Assume these tangents meet at E on BD (without loss of generality we can assume E is on the side of D.)
Then the alternate segment theorem tells us triangles EAD and EBA are similar, and also ECD and EBC are similar.
So AE/BE=AD/AB and CE/BE=CD/BC.
As AE and CE are both tangents to the same circle from the same point, they are equal, and we can conclude AD/AB = CD/BC => AD.BC=AB.CD.
Conversely, suppose AD.BC=AB.CD.
Let X be the intersection of the tangent at A with BD and Y be the intersection of the tangent at C with BD.
Then we get XAD and XBA similar and YCD and YBC similar.
Hence DX/BX=(AX/BX).(DX/AX)=(AD/AB)^2=(CD/BC)^2=(CY/BY).(DY/CY)=DY/BY.
But the quantity DP/BP increases as you move P further away from the circle, so we must have X=Y as claimed.
(Note the this is only truly if and only if we interpret parallel lines as meeting at infinity, and we then allow for the tangents to meet the secant at equal distances away from the circle on either side. Eg a square obviously has products of opposite sides equal, but tangents at opposite vertices are parallel.)
Sure.
So let ABCD be the cyclic quad in anticlockwise order, and we are drawing tangents at A and C.
Assume these tangents meet at E on BD (without loss of generality we can assume E is on the side of D.)
Then the alternate segment theorem tells us triangles EAD and EBA are similar, and also ECD and EBC are similar.
So AE/BE=AD/AB and CE/BE=CD/BC.
As AE and CE are both tangents to the same circle from the same point, they are equal, and we can conclude AD/AB = CD/BC => AD.BC=AB.CD.
Conversely, suppose AD.BC=AB.CD.
Let X be the intersection of the tangent at A with BD and Y be the intersection of the tangent at C with BD.
Then we get XAD and XBA similar and YCD and YBC similar.
Hence DX/BX=(AX/BX).(DX/AX)=(AD/AB)^2=(CD/BC)^2=(CY/BY).(DY/CY)=DY/BY.
But the quantity DP/BP increases as you move P further away from the circle, so we must have X=Y as claimed.
(Note the this is only truly if and only if we interpret parallel lines as meeting at infinity, and we then allow for the tangents to meet the secant at equal distances away from the circle on either side. Eg a square obviously has products of opposite sides equal, but tangents at opposite vertices are parallel.)
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
First note that there is no solution with either of x,y equal to 0.
Case A: x negative, y positive
Unless y=1, only one side will be an integer. A trivial check shows there is no solution with y=1 and x negative.
Case B: x, y both negative.
By factoring out the (-1)^x and (-1)^y, we get a 1-1 correspondence between negative solution pairs and positive solution pairs with both variables having the same parity. This reduces the problem to...
Case C: x,y positive integers.
Wlog assume x < y.
By inspection there is no solution with x=1.
The condition is then equivalent to x/log(x)=y/log(y).
But differentiating shows that f(t)=t/log(t) decreases from 1 to e and increases thereafter, so we must have 1 < x < e. So x=2 is the only possible source of solutions and there is exactly one real solution to x^2=2^x in the interval (e,infinity).
As it happens, this solution is an integer! It is 4.
Hence the only solution pairs are (2,4),(4,2),(-2,-4),(-4,-2).
Cool question! I think I have covered cases correctly: \ $where$ \ x^y = y^x \ $and$ \ x \neq y )
First note that there is no solution with either of x,y equal to 0.
Case A: x negative, y positive
Unless y=1, only one side will be an integer. A trivial check shows there is no solution with y=1 and x negative.
Case B: x, y both negative.
By factoring out the (-1)^x and (-1)^y, we get a 1-1 correspondence between negative solution pairs and positive solution pairs with both variables having the same parity. This reduces the problem to...
Case C: x,y positive integers.
Wlog assume x < y.
By inspection there is no solution with x=1.
The condition is then equivalent to x/log(x)=y/log(y).
But differentiating shows that f(t)=t/log(t) decreases from 1 to e and increases thereafter, so we must have 1 < x < e. So x=2 is the only possible source of solutions and there is exactly one real solution to x^2=2^x in the interval (e,infinity).
As it happens, this solution is an integer! It is 4.
Hence the only solution pairs are (2,4),(4,2),(-2,-4),(-4,-2).
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon - Advanced Level
Quite interesting how numbers like 4 and 2 can come out of something that seems so simple
Yep pretty similar to my solution!
Quite interesting how numbers like 4 and 2 can come out of something that seems so simple
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
Definitely! It feels more like a coincidence than anything actually deep, but still.
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
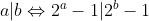
for positive integers a and b. Note that if this is true, then any common factor of your two quantities must also be a common factor of two distinct primes, and hence can only be 1.
The)
part was proven in the last page of this marathon. I'll show the other direction now.
We can write b=aq+r uniquely, with q,r non-negative integers and
If
, then -(2^{aq}-1)))
from the result.
So)
.
But since the LHS is odd, it is coprime to any power of 2. So we get
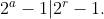
As the RHS is strictly less than the LHS, this is only possible if the RHS is 0. Ie r=0, which means that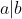
as claimed.
I'll prove the stronger result that
for positive integers a and b. Note that if this is true, then any common factor of your two quantities must also be a common factor of two distinct primes, and hence can only be 1.
The
We can write b=aq+r uniquely, with q,r non-negative integers and
If
So
But since the LHS is odd, it is coprime to any power of 2. So we get
As the RHS is strictly less than the LHS, this is only possible if the RHS is 0. Ie r=0, which means that
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2014 4U Marathon - Advanced Level
Let q(n)=(2n+1)p(n).
Now if flipping (n+1) coins is to give an odd number of heads, either our final coin is a head and we have an even number of heads in our first n coins, or our final coin is a tail and we have an odd number of heads in our first n coins.
So
p(n+1)=(1-p(n))/(2n+3)+p(n)(2n+2)/(2n+3)=(1+(2n+1)p(n))/(2n+3).
But this is just saying q(n+1)=q(n)+1.
As p(1)=1/3, we have q(1)=1 and hence q(n)=n.
This lets us conclude that=\frac{n}{2n+1}.)
Let p(n) be the probability of flipping an odd number of heads with n such coins.Here is a nice probability question
Let q(n)=(2n+1)p(n).
Now if flipping (n+1) coins is to give an odd number of heads, either our final coin is a head and we have an even number of heads in our first n coins, or our final coin is a tail and we have an odd number of heads in our first n coins.
So
p(n+1)=(1-p(n))/(2n+3)+p(n)(2n+2)/(2n+3)=(1+(2n+1)p(n))/(2n+3).
But this is just saying q(n+1)=q(n)+1.
As p(1)=1/3, we have q(1)=1 and hence q(n)=n.
This lets us conclude that
- Status