Re: MX2 2015 Integration Marathon
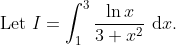
Let u = ln x. So x = eu ⇒ dx = eu du.
When x = 1, u = 0, and when x = 3, u = ln 3.
 .
.
Now, using the fact that \text{ d}x =\int_0^{a} f(a-x) \text{ d}x ) , we have
, we have
\text{e}^{\ln 3 - u}}{3+\text{e}^{2{(\ln 3 - u)}}} \text{ d}u. )
Since eln 3 - u = eln 3.e-u = 3e-u, we have
3\text{e}^{-u}}{3+{(3\text{e}^{-u})}^2} \text{ d}u )
 \cdot 3\text{e}^{-u}}{3+9\text{e}^{-2u}} \text{ d}u - \int_0^{\ln 3}\frac{u\cdot 3\text{e}^{-u}}{3+9\text{e}^{-2u}} \text{ d}u )
 \text{e}^{-u}}{1+3\text{e}^{-2u}} \text{ d}u - \int_0^{\ln 3}\frac{u\text{e}^{-u}}{1+3\text{e}^{-2u}} \text{ d}u )
 \text{e}^{-u}}{1+3\text{e}^{-2u}} \text{ d}u - \int_0^{\ln 3}\frac{u\text{e}^{u}}{\text{e}^{2u}+3} \text{ d}u ) (multiplying the numerator and denominator of the integrand of the second integral on the RHS by e2u )
(multiplying the numerator and denominator of the integrand of the second integral on the RHS by e2u )
 \text{e}^{-u}}{1+3\text{e}^{-2u}} \text{ d}u - I )
 \text{e}^{-u}}{1+3\text{e}^{-2u}} \text{ d}u. )
This is pretty easy to integrate now. Let v = e-u ⇒ -dv = e-u du and change the limits of integration, so
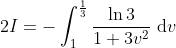
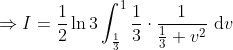
 \right ]_\frac{1}{3} ^1 )
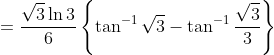
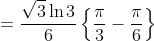
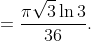
lol a 100% magic done by substitution. anyone can find a way to play this magic:

Let u = ln x. So x = eu ⇒ dx = eu du.
When x = 1, u = 0, and when x = 3, u = ln 3.
Now, using the fact that
Since eln 3 - u = eln 3.e-u = 3e-u, we have
This is pretty easy to integrate now. Let v = e-u ⇒ -dv = e-u du and change the limits of integration, so
