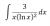- Joined
- Feb 16, 2005
- Messages
- 8,500
- Gender
- Male
- HSC
- 2006
Post any questions within the scope and level of Mathematics Extension 1. Once a question is posted, it needs to be answered before the next question is raised.
I encourage all current students in particular to participate in this marathon.
To start off:

I encourage all current students in particular to participate in this marathon.
To start off:
Last edited: