Since is continuous on
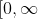)
, it continuous on
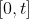
for any positive real number
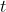
. If
)
is never positive, then clearly attains a maximum (0) at
x = 0. So assume is positive somewhere in the interval
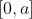
, where

is some positive real number.
By the Extreme Value Theorem, attains a maximum value
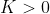
on
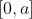
, say at
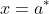
. Since
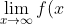=0)
, it means that for all

greater than some positive number
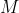
(which must be greater than
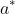
), we will have
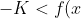<K)
. Now consider the interval
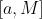
. By the Extreme Value Theorem, attains a maximum
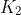
on here. If
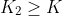
, then attains the maximum value
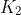
on the interval
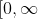)
(since
\leq K \leq K_2)
for all
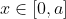
and
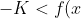<K\leq K_2)
for all
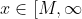)
). Otherwise (i.e.
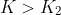
), attains the maximum value
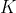
on
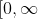)
, since
\leq K)
for all
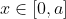
,
\leq K_2 < K)
for all
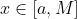
, and
<K)
for all
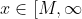)
. In either case, indeed attains a maximum on
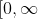)
(the maximum being
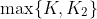
).