Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2016 MX2 Marathon (archive) (1 Viewer)
- Thread starter Trebla
- Start date
- Status
- Not open for further replies.
Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon
^2$, leaving your answer in the form $a+b\sqrt{c}$,$\\$where $c$ is a square free integer, and $a,b$, are integers.)
Last edited:
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2016 4U Marathon
.Just a reminder to please stick to questions related to the HSC syllabus.
Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon
You're one to talk, you didn't even do that in the 2014 and 2015 marathons.
porcupinetree
not actually a porcupine
- Joined
- Dec 12, 2014
- Messages
- 664
- Gender
- Male
- HSC
- 2015
Re: HSC 2016 4U Marathon
Leaked question 11(a) of 2016 4U HSC exam
DatAtarLyfe
Booty Connoisseur
- Joined
- Mar 10, 2015
- Messages
- 1,802
- Gender
- Female
- HSC
- 2016
Re: HSC 2016 4U Marathon
whatLeaked question 11(a) of 2016 4U HSC exam
Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon
nekminnit
actually thoughLeaked question 11(a) of 2016 4U HSC exam
nekminnit
Re: HSC 2016 4U Marathon
 = \cos \omega t$. Let's just consider $0\leq t \leq \frac{\pi}{2\omega}$ (so the first quarter-cycle), as after this everything repeats symmetrically. We will find the fraction of time the particle spends in our chosen subintervals. The particle reaches the end of our subinterval when $x(t) = \cos \omega t= 1-\frac{L}{2}\Longleftrightarrow t=\frac{\cos ^{-1}\left(1-\frac{L}{2}\right)}{\omega}$. Hence the proportion of time $\varpi$ in the first quarter (and by symmetry overall) that the particle spends in our subintervals is $\varpi = \frac{\frac{\cos ^{-1}\left(1-\frac{L}{2}\right)}{\omega}}{\frac{\pi}{2\omega}}=\frac{2}{\pi}\cos ^{-1}\left(1-\frac{L}{2}\right)$.$)
$. (It is always a good idea to check if extreme cases work. If $L=2$, i.e. we covered the whole interval, the probability should be 1, and substituting $L=2$ into our formula indeed gives $1$. If $L=0$, the probability should be $0$, and indeed it is if we substitute $L=0$.) So our expected profit is $\frac{1}{L}\cdot \frac{2}{\pi}\cos ^{-1}\left(1-\frac{L}{2}\right) -1$ (subtracting the 1 as this is the game's fee), and as $L\to 0^{+}$, $\frac{\cos ^{-1}\left(1-\frac{L}{2}\right)}{L}$ has limit$)
}{L} &= \lim_{L \to 0^{+}} \frac{ -\frac{1}{2}\cdot \frac{-1}{\sqrt{1-\left(1-\frac{L}{2}\right)^2}}}{1} \quad (\text{using L'Hospital's rule, as both numerator and denominator go to }0) \\ &= \lim_{L\to 0^{+}} \frac{1}{2\sqrt{1-\left(1-\frac{L}{2}\right)^2}} \\ &= \infty.\end{align*}$$)
Hence we can make the expected profit arbitrarily large.
I believe you can obtain an arbitrarily large expected profit by choosing your subintervals to be arbitrarily small and at the endpoints of the whole interval, e.g. choose two intervals like this: [1, 1 – L/2] and [-1, -1 + L/2], and make L arbitrarily small (the total length of these subintervals is L). The motivation for placing them at the ends is that a simple harmonic oscillator spends more time per unit length at the ends, as it is slower there, so any length of subinterval we use should be chosen as close to the ends as possible. We will show that this allows for an arbitrarily high expected value.A game of chance uses a simple harmonic oscillator. Its amplitude of oscillation is 1 but its frequency is unknown to you.
To play the game, you have to pay $1, and you get to choose a finite number of closed subintervals of [-1,1].
You win if after a random large amount of time, the oscillating particle lies in one of your subintervals, and you win $(1/L) where L is the sum of the lengths of your subintervals. So for example, if you were to cover the whole interval [-1,1] with a single subinterval, you will always "win", but as you only get $0.50 of your $1 back, this is not a good strategy!
Q/ How large an expected profit can you obtain with a well chosen bet? Provide proof.
Hence we can make the expected profit arbitrarily large.
Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon
What would happen if it didn't have a simple frequency? e.g. cos(t^2) or something like that.I believe you can obtain an arbitrarily large expected profit by choosing your subintervals to be arbitrarily small and at the endpoints of the whole interval, e.g. choose two intervals like this: [1, 1 – L/2] and [-1, -1 + L/2], and make L arbitrarily small (the total length of these subintervals is L). The motivation for placing them at the ends is that a simple harmonic oscillator spends more time per unit length at the ends, as it is slower there, so any length of subinterval we use should be chosen as close to the ends as possible. We will show that this allows for an arbitrarily high expected value.
Hence we can make the expected profit arbitrarily large.
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2016 4U Marathon
Good stuff Integrand, that is exactly correct.
Of course all this question really amounts to is the statement that the PDF of the particles position at a random large time tends to infinity as you approach +-1.
Good stuff Integrand, that is exactly correct.
Of course all this question really amounts to is the statement that the PDF of the particles position at a random large time tends to infinity as you approach +-1.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2016 4U Marathon
Try to show this yourself.
To find a g where sin(g(t)) (with g(t) increasing) did not have this property, you could cook up g so that the particle slows down heaps every time it is near zero for instance.
For simple things like power functions, you would still be able to get arbitrarily large EV, but the calculations are messier.What would happen if it didn't have a simple frequency? e.g. cos(t^2) or something like that.
Try to show this yourself.
To find a g where sin(g(t)) (with g(t) increasing) did not have this property, you could cook up g so that the particle slows down heaps every time it is near zero for instance.
Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon
 = t+\sin{t})
I can't seem to find a simple function where the particle spends most of it's time near the origin...
Time to go on a function hunt.
Hmm... interesting... I have found a function where the particle spends significantly more time at -1 than 1...
For simple things like power functions, you would still be able to get arbitrarily large EV, but the calculations are messier.
Try to show this yourself.
To find a g where sin(g(t)) (with g(t) increasing) did not have this property, you could cook up g so that the particle slows down heaps every time it is near zero for instance.
I can't seem to find a simple function where the particle spends most of it's time near the origin...
Time to go on a function hunt.
Hmm... interesting... I have found a function where the particle spends significantly more time at -1 than 1...
Last edited:
Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon
 \equiv t+\sin{t}+\sin{\left(t+\sin{t}\right)}\\ \sin(g(t)) $ results in a particle that spends a highly disproportionate amount of time near the origin. Now, I presume ''simple'' harmonic oscillation is always a linear input of time?$ )
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2016 4U Marathon
Yes simple harmonic motion is just the case where g is a linear polynomial in time, ie the case treated by Integrand.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2016 4U Marathon
A classic:
1. Use the trapezoidal approximation to show that there exists a positive constant A such that for all positive integers n.
for all positive integers n.
2. Using another inequality coming from integration, show there exists a positive constant B such that
3. By considering the binomial coefficient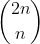 , find
, find  (You may assume without proof that this limit exists.)
(You may assume without proof that this limit exists.)
Hint for 3: You might find it useful to think about powers of trig functions.
E. (Extension) It is a basic lemma in real analysis that if a sequence of real numbers is monotonic and bounded, it is convergent. Using this lemma or otherwise, fill in the gap in Q3 and prove that exists.
exists.
A classic:
1. Use the trapezoidal approximation to show that there exists a positive constant A such that
2. Using another inequality coming from integration, show there exists a positive constant B such that
3. By considering the binomial coefficient
Hint for 3: You might find it useful to think about powers of trig functions.
E. (Extension) It is a basic lemma in real analysis that if a sequence of real numbers is monotonic and bounded, it is convergent. Using this lemma or otherwise, fill in the gap in Q3 and prove that
Last edited:
Nailgun
Cole World
- Joined
- Jun 14, 2014
- Messages
- 2,190
- Gender
- Male
- HSC
- 2016
Last edited:
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2016 4U Marathon
 ?
?
I had to help a student do this maths question just now. I feel it would be good to leave it on the 4U marathon as an instructive exercise for any E3 or above aiming student to attempt.

leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Re: HSC 2016 4U Marathon
But I want the 2016ers to attempt the question with full working. If they don't want to upload a diagram they can just briefly explain it
Yes lol
But I want the 2016ers to attempt the question with full working. If they don't want to upload a diagram they can just briefly explain it
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2016 4U Marathon
 you don't need to
you don't need to
I didn't use a diagramYes lol
But I want the 2016ers to attempt the question with full working. If they don't want to upload a diagram they can just briefly explain it
- Status
- Not open for further replies.

