asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
b) A tangent to the parabola  meets the hyperbola
meets the hyperbola  in the points P, Q.
in the points P, Q.
i) Show that the equation of the tangent at) on the parabola is
on the parabola is 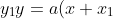)
ii) Show that the x coordinates of P and Q are given by the equation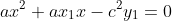
iii) Deduce the cartesian equation of the locus of the midpoint M of the interval PQ.
I've done ii) and I got that equation. Stuck on iii)
I noticed that the equation is a quadratic in x, so that the sum of roots divided by 2 is the midpoint, so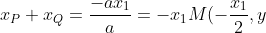) . Now PQ is on the tangent, so
. Now PQ is on the tangent, so 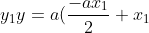 \\ y = \frac{ax_1}{2y_1}=\frac{ax}{y_1}) And there's where I'm stuck...don't know how to get rid of the y1..
And there's where I'm stuck...don't know how to get rid of the y1..
Any help is appreciated!
i) Show that the equation of the tangent at
ii) Show that the x coordinates of P and Q are given by the equation
iii) Deduce the cartesian equation of the locus of the midpoint M of the interval PQ.
I've done ii) and I got that equation. Stuck on iii)
I noticed that the equation is a quadratic in x, so that the sum of roots divided by 2 is the midpoint, so
Any help is appreciated!
Last edited:
