HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
A ball is projected from a point on the ground, distance a from the foot of a vertical wall of height b. The ball is projected at an elevation 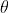 with speed V.
with speed V.
a) Find how high above the wall the ball passes it.
b) If the ball just cleans the wall, prove the greatest height reached is:
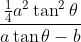
a) Find how high above the wall the ball passes it.
b) If the ball just cleans the wall, prove the greatest height reached is:
