-
Best of luck to the class of 2024 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Another question (Integration) (1 Viewer)
- Thread starter BlueGas
- Start date
Incorrect graph, there it should pass the origin and looks like a stat pt at x=1 and x= -1. With this question you need to take note of the area under the positive axis.I need help with question 5. d), I also want to know if the graph I drew was correct for the question or not, thanks.


Last edited:
BlueGas
Well-Known Member
- Joined
- Sep 20, 2014
- Messages
- 2,448
- Gender
- Male
- HSC
- N/A
But I did like a table of values thing where I subbed in x=2, x=1, x=0, x=-1 and x=-2 and the result was the graph I drew. I just looked at the graph on Google now but the results I got from the table of values were plotted on the graph. I just don't get how the graph is wrong even though it is...Incorrect graph, there it should pass the origin and a jump that looks like a stat pt at x=1. With this question you need to take note of the area under the positive axis.
enigma_1
~~~~ Miss Cricket ~~~~
It should look like this: https://www.google.com.au/#q=y=x^3+-x
Always check with wolfram alpha. Here you go http://www.wolframalpha.com/input/?i=y=x((x^2)-1)But I did like a table of values thing where I subbed in x=2, x=1, x=0, x=-1 and x=-2 and the result was the graph I drew. I just looked at the graph on Google now but the results I got from the table of values were plotted on the graph. I just don't get how the graph is wrong even though it is...
BlueGas
Well-Known Member
- Joined
- Sep 20, 2014
- Messages
- 2,448
- Gender
- Male
- HSC
- N/A
But in the exam I can't use wolfram how am I meant to know how to graph this sort of question if even the table of values gave me the wrong graph.Always check with wolfram alpha. Here you go http://www.wolframalpha.com/input/?i=y=x((x^2)-1)
enigma_1
~~~~ Miss Cricket ~~~~
factorise the equation firstly: y = x(x^2 -1) = x(x-1)(x+1)But in the exam I can't use wolfram how am I meant to know how to graph this sort of question if even the table of values gave me the wrong graph.
from there, you find the x intercepts by letting y=0, so x ints are x= -1, 0 and 1.
Since there is no negative in front of the "x" you know that the graph will be going diagonal from the top right to the bottom left (like a line with positive gradient). Then you basically draw in the middle bit with the line passing through each of the x intercepts with the loops etc.
when x = -2, y = -6But what I don't get is that why couldn't the table of values help me in graphing this sort of question?
when x = -1, y = 0
when x = -1/2, y = 3/8
when x = 0, y = 0
when x = 1/2, y= -3/8
when x = 1, y = 0
when x = -2, y = 0
Judging by your graph, you missed out what happens when x = - 1/2 and x = 1/2
BlueGas
Well-Known Member
- Joined
- Sep 20, 2014
- Messages
- 2,448
- Gender
- Male
- HSC
- N/A
I just got told that if a graph has x^3 it starts above the X axis from the right but Google and wolfram say otherwise. I'm kind of confused. ..when x = -2, y = -6
when x = -1, y = 0
when x = -1/2, y = 3/8
when x = 0, y = 0
when x = 1/2, y= -3/8
when x = 1, y = 0
when x = -2, y = 0
Judging by your graph, you missed out what happens when x = - 1/2 and x = 1/2
Why not graph it by finding the stat pts and poi.I just got told that if a graph has x^3 it starts above the X axis from the right but Google and wolfram say otherwise. I'm kind of confused. ..
The function is  = x(x^2 -1) = x(x+1)(x-1) ) (using difference of two squares). So the polynomial has roots at
(using difference of two squares). So the polynomial has roots at  . also, the function is odd (
. also, the function is odd ( = -f(-x) ) ), so is symmetric about the origin. As
), so is symmetric about the origin. As  \to \pm \infty ) . This is enough information to sketch the curve (you don't need to and shouldn't use calculus, since you just need the rough shape).
. This is enough information to sketch the curve (you don't need to and shouldn't use calculus, since you just need the rough shape).
And there's no stationary points at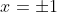 . all the roots are single roots, so the curve cuts the x-axis at these points like a straight line.
. all the roots are single roots, so the curve cuts the x-axis at these points like a straight line.
And there's no stationary points at
BlueGas
Well-Known Member
- Joined
- Sep 20, 2014
- Messages
- 2,448
- Gender
- Male
- HSC
- N/A
I understand the polynomial has roots at x=, x=1, x=-1 but what I don't get is how would you know that there are loops on the graph?The function is(using difference of two squares). So the polynomial has roots at
. also, the function is odd (
), so is symmetric about the origin. As
. This is enough information to sketch the curve (you don't need to and shouldn't use calculus, since you just need the rough shape).
And there's no stationary points at. all the roots are single roots, so the curve cuts the x-axis at these points like a straight line.
enigma_1
~~~~ Miss Cricket ~~~~
Since the roots are only -1, 0 and 1 you know that when you're drawing the graph, it's going to cut each point like legit intersect it and go right through it like a loop.I understand the polynomial has roots at x=, x=1, x=-1 but what I don't get is how would you know that there are loops on the graph?
If you have like -1, -1, 0 and 1 as your roots, since there are two -1s, the graph does not cut the x intercept at x= -1 and instead it just touches that point like how the y=x^2 parabola touches the origin.
These are pretty basic concepts which you could look through in your textbook tbh or youtube videos as you need to know how to graph all sorts of functions like second nature.
BlueGas
Well-Known Member
- Joined
- Sep 20, 2014
- Messages
- 2,448
- Gender
- Male
- HSC
- N/A
I do know how to graph equations when they ask for stationary points, maximum/minimum, pt of inflex, etc. But this type of graphing for integration confuses me, I don't want to be doing the same method of graphing in calculus for integration, it takes up alot of time and I'm sure there's a faster way to graph when answering integration questions.Since the roots are only -1, 0 and 1 you know that when you're drawing the graph, it's going to cut each point like legit intersect it and go right through it like a loop.
If you have like -1, -1, 0 and 1 as your roots, since there are two -1s, the graph does not cut the x intercept at x= -1 and instead it just touches that point like how the y=x^2 parabola touches the origin.
These are pretty basic concepts which you could look through in your textbook tbh or youtube videos as you need to know how to graph all sorts of functions like second nature.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
A problem like question 5 (d) would not be asked in a 2U examination paper anyway because it's a cubic polynomial, the graph of which isn't in the 2U course without the assistance of calculus to sketch it.
enigma_1
~~~~ Miss Cricket ~~~~
For integration it's beneficial to roughly sketch out what the graph would look like. You don't need to figure out stationary points or anything, just find the x intercepts and whether the leading coefficient is positive or negative and whether there is a y intercept. Using all that info and how many roots the equation has, you can draw up a quick sketch of any graph for integration purposes to visualise what's happening.I do know how to graph equations when they ask for stationary points, maximum/minimum, pt of inflex, etc. But this type of graphing for integration confuses me, I don't want to be doing the same method of graphing in calculus for integration, it takes up alot of time and I'm sure there's a faster way to graph when answering integration questions.
BlueGas
Well-Known Member
- Joined
- Sep 20, 2014
- Messages
- 2,448
- Gender
- Male
- HSC
- N/A
So basically any equation that has a cubic polynomial won't be in the 2U exam? That's a relief. Because I know how to sketch x^2 and anything above I can't.A problem like question 5 (d) would not be asked in a 2U examination paper anyway because it's a cubic polynomial, the graph of which isn't in the 2U course without the assistance of calculus to sketch it.

