any suggestions about how to approach this question on continuous pdf? (1 Viewer)

Fizsi · Sep 15, 2020

A piecewise function f(x) is defined as follows

f(x)=-x+a ,x<0
f(x)= 1/x+a, x greater or equal to 0
What value or values of a make the function continous?

cossine · Sep 15, 2020

lim x->0^+ (1/x + a) = infinity

lim x-> 0^- (-x+a) = a

Therefore there is no value of "a" that makes the function continuous as the left and right one-sided limits are different.

CM_Tutor · Sep 27, 2020

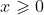
I think that @Fizsi means the piece of the function for $x \geqslant 0$ to be

$f(x) = \frac{1}{x+a}$

rather than

$f(x) = \frac{1}{x}+a$

because, as @cossine has noted, this second interpretation leads to no solution being possible.

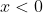
Assuming the first interpretation, for $x < 0$ , we have

$\lim_{x \to 0^-}{f(x)}=\lim_{x \to 0^-}{(x+a)}=0+a=a$

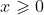
and for $x \geqslant 0$ , we have

$\lim_{x \to 0^+}{f(x)}=\lim_{x \to 0^+}{\frac{1}{x+a}} = \frac{1}{0+a} = \frac{1}{a}$

For $f(x)$ to be continuous, the branches must meet and the limits must be the same, and thus:

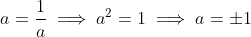
$a = \frac{1}{a} \implies a^2 = 1 \implies a=\pm1$ .

Make a Difference – Donate to Bored of Studies!

any suggestions about how to approach this question on continuous pdf? (1 Viewer)

Fizsi

New Member

cossine

Well-Known Member

CM_Tutor

Moderator

Users Who Are Viewing This Thread (Users: 0, Guests: 1)