are monic polynomials strictly polys with leading coefficients of positive one, or can it be -1 as well?? (1 Viewer)

anonymoushehe · Oct 19, 2023

^^^ (sorry if its a dumb q)

scaryshark09 · Oct 19, 2023

only positive 1

Luukas.2 · Oct 20, 2023

If we consider a cubic, the polynomial

$P(x) = Ax^3 + Bx^2 + Cx + D$

being monic requires that $A = 1$ .

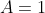
However, if we have a cubic polynomial in an equation, like

$2x^2 - x^3 + 7x - 4 = 0$

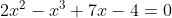
then it could be described as monic because it can be re-written as

$x^3 - 2x^2 - 7x + 4 = 0$

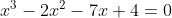
and hence taken as

$P(x) = x^3 - 2x^2 - 7x + 4 \qquad \text{where} \qquad P(x) = 0$

and in this case $P(x)$ is clearly monic. Having said that, any polynomial equation can be re-written as a monic polynomial of the same degree by dividing by the stated leading coefficient:

$\begin{align*} 4x^5 - 12x^6 + 48x^2 - 17x^3 - 6 &= 0 \\ \\ \text{Dividing by $-12$}: \qquad \frac{4x^5}{-12} - \frac{12x^6}{-12} + \frac{48x^2}{-12} - \frac{17x^3}{-12} - \frac{6}{-12} &= \frac{0}{-12} \\ \\ \text{Resolving double negatives}: \qquad - \frac{4x^5}{12} + \frac{12x^6}{12} - \frac{48x^2}{12} + \frac{17x^3}{12} + \frac{6}{12} &= 0 \\ \\ \text{Removing pronumerals from fractions}: \qquad - \frac{4}{12}x^5 + \frac{12}{12}x^6 - \frac{48}{12}x^2 + \frac{17}{12}x^3 + \frac{6}{12} &= 0 \\ \\ \text{Simplifying fractions}: \qquad - \frac{1}{3}x^5 + 1 \times x^6 - 4 \times x^2 + \frac{17}{12}x^3 + \frac{1}{2} &= 0 \\ \\ \text{Arranging in decreasing powers}: \qquad x^6 - \frac{1}{3}x^5 +\frac{17}{12}x^3 - 4x^2 + \frac{1}{2} &= 0 \end{align*}$

and the resulting equation is a monic polynomial of degree 6.

are monic polynomials strictly polys with leading coefficients of positive one, or can it be -1 as well?? (1 Viewer)

anonymoushehe

Member

scaryshark09

∞∆ who let 'em cook dis long ∆∞

Luukas.2

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 1)