https://drive.google.com/open?id=1NRMNrcOf0uy0tUMH4cTgUEj_eegL2jMv
Can you please provide working out.
Thanks
Can you please provide working out.
Thanks
-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Binomial Theorem (1 Viewer)
- Thread starter Andy005
- Start date
i) Using the binomial theorem you have
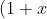^{n+k} =\sum_{r=0}^{n+k} \binom{n+k}{r} x^r )
Equate the co-efficients of
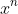
on both sides using the above for 
.
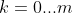
On the LHS we have
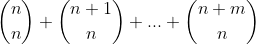
and on the RHS we want the co-efficients of
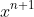
since we are dividing by 
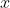
. The second binomial clearly does not have a co-efficient of 
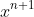
so we need only to find the required co-efficient of the first binomial, which is
.
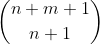
ii) from i) set
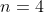
This gives
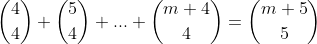
Subtract 1 and note that
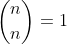
for all 
.
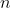
This gives
Rewriting in sigma notation, we get:
Rewrite the binomial on the LHS:
!4!} = \binom{m+5}{5} - 1)
Multiply both sides by
:
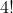
!} = 24\left(\binom{m+5}{5} - 1\right))
And rewrite the LHS:
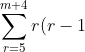(r-2)(r-3) = 24\left(\binom{m+5}{5} - 1\right))
Equate the co-efficients of
On the LHS we have
and on the RHS we want the co-efficients of
ii) from i) set
This gives
Subtract 1 and note that
This gives
Rewriting in sigma notation, we get:
Rewrite the binomial on the LHS:
Multiply both sides by
And rewrite the LHS:
Last edited: