Kingportable
Member
- Joined
- Jun 26, 2011
- Messages
- 172
- Gender
- Male
- HSC
- 2012
Using Tk+1 = nCk . a^n-k . b^k
how do you find the x^-3/2 term of (x^(1/2)/2 - 4/x^(1/4))^9
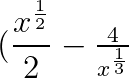^9 , x^{-\frac{3}{2}})
<a href="http://www.codecogs.com/eqnedit.php?latex=\dpi{120} $This is what i did$\\ T_{k@plus;1} = C _{k}^{9}\textrm{}(\tfrac{x\frac{1}{2}}{2})^{9-k}(\frac{4}{x^\frac{1}{4}})^{9}\\ T_{k@plus;1} = C _{k}^{9}(\frac{1}{2})^{9-k}.(-4)^k.(x)^{\frac{9}{2}-k}.(x)^{\frac{1}{4}}\\ T_{k@plus;1} = C _{k}^{9}(\frac{1}{2})^{9-k}.(-4)^k.(x)^{\frac{9}{2}-\frac{9}{k}-\frac{k}{4}}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\dpi{120} $This is what i did$\\ T_{k+1} = C _{k}^{9}\textrm{}(\tfrac{x\frac{1}{2}}{2})^{9-k}(\frac{4}{x^\frac{1}{4}})^{9}\\ T_{k+1} = C _{k}^{9}(\frac{1}{2})^{9-k}.(-4)^k.(x)^{\frac{9}{2}-k}.(x)^{\frac{1}{4}}\\ T_{k+1} = C _{k}^{9}(\frac{1}{2})^{9-k}.(-4)^k.(x)^{\frac{9}{2}-\frac{9}{k}-\frac{k}{4}}" title="\dpi{120} $This is what i did$\\ T_{k+1} = C _{k}^{9}\textrm{}(\tfrac{x\frac{1}{2}}{2})^{9-k}(\frac{4}{x^\frac{1}{4}})^{9}\\ T_{k+1} = C _{k}^{9}(\frac{1}{2})^{9-k}.(-4)^k.(x)^{\frac{9}{2}-k}.(x)^{\frac{1}{4}}\\ T_{k+1} = C _{k}^{9}(\frac{1}{2})^{9-k}.(-4)^k.(x)^{\frac{9}{2}-\frac{9}{k}-\frac{k}{4}}" /></a>
how do you find the x^-3/2 term of (x^(1/2)/2 - 4/x^(1/4))^9
<a href="http://www.codecogs.com/eqnedit.php?latex=\dpi{120} $This is what i did$\\ T_{k@plus;1} = C _{k}^{9}\textrm{}(\tfrac{x\frac{1}{2}}{2})^{9-k}(\frac{4}{x^\frac{1}{4}})^{9}\\ T_{k@plus;1} = C _{k}^{9}(\frac{1}{2})^{9-k}.(-4)^k.(x)^{\frac{9}{2}-k}.(x)^{\frac{1}{4}}\\ T_{k@plus;1} = C _{k}^{9}(\frac{1}{2})^{9-k}.(-4)^k.(x)^{\frac{9}{2}-\frac{9}{k}-\frac{k}{4}}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\dpi{120} $This is what i did$\\ T_{k+1} = C _{k}^{9}\textrm{}(\tfrac{x\frac{1}{2}}{2})^{9-k}(\frac{4}{x^\frac{1}{4}})^{9}\\ T_{k+1} = C _{k}^{9}(\frac{1}{2})^{9-k}.(-4)^k.(x)^{\frac{9}{2}-k}.(x)^{\frac{1}{4}}\\ T_{k+1} = C _{k}^{9}(\frac{1}{2})^{9-k}.(-4)^k.(x)^{\frac{9}{2}-\frac{9}{k}-\frac{k}{4}}" title="\dpi{120} $This is what i did$\\ T_{k+1} = C _{k}^{9}\textrm{}(\tfrac{x\frac{1}{2}}{2})^{9-k}(\frac{4}{x^\frac{1}{4}})^{9}\\ T_{k+1} = C _{k}^{9}(\frac{1}{2})^{9-k}.(-4)^k.(x)^{\frac{9}{2}-k}.(x)^{\frac{1}{4}}\\ T_{k+1} = C _{k}^{9}(\frac{1}{2})^{9-k}.(-4)^k.(x)^{\frac{9}{2}-\frac{9}{k}-\frac{k}{4}}" /></a>
Last edited:
