-
Looking for HSC notes and resources? Check out our Notes & Resources page
Calculus Maxima and Minima (1 Viewer)
- Thread starter Aysce
- Start date
funnytomato
Active Member
- Joined
- Jan 21, 2011
- Messages
- 847
- Gender
- Male
- HSC
- 2010
quick question - what textbooks are you using?Hey guys, I was wondering if anyone happens to have like a guide for doing these sorts of problems, as neither of my textbooks include anything about maxima or minima, and I am sorta short of time
Shadowdude
Cult of Personality
- Joined
- Sep 19, 2009
- Messages
- 12,143
- Gender
- Male
- HSC
- 2010
Minima and maxima are done through derivatives.
Differentiate the function, solve it for zero to find the x value where the function has a stationary point.
Differentiate again to get a second derivative, sub in the 'x' values where the function has a stationary point - and if the double derivative is positive, then the function has a minimum, and if the double derivative is negative, the function has a maximum at that x value.
Differentiate the function, solve it for zero to find the x value where the function has a stationary point.
Differentiate again to get a second derivative, sub in the 'x' values where the function has a stationary point - and if the double derivative is positive, then the function has a minimum, and if the double derivative is negative, the function has a maximum at that x value.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
First of all, you must find the first derivative. For stationary points, set the first derivative to zero and find the x-values. Hence substitute into your original equation to find the corresponding y values.
Second step: To determine the nature of the stationary points, you must do either:
If , a maximum turning point occurs.
, a maximum turning point occurs.
If , a minimum turning point occurs.
, a minimum turning point occurs.
If , a POSSIBLE inflexion point occurs. (In this case you must test to the left and to the right of the value. This will probably NEVER happen if it asks you to find maximum or minimum values.)
, a POSSIBLE inflexion point occurs. (In this case you must test to the left and to the right of the value. This will probably NEVER happen if it asks you to find maximum or minimum values.)
The steps above is to see if the value at that coordinate is a maximum or minimum.
[Note: I am assuming you have got the formula before differentiating the function. Also if you take points to the left and right of a value you must take it significantly close to it. (Eg. Testing to the left and right of 5 means substitute values close to it such as 4.9 and 5.1)]
Example question: With reference to this beautiful picture I drew!
 (http://imageshack.us/f/695/foraysce.jpg/)
(http://imageshack.us/f/695/foraysce.jpg/)
A square tin plate of length 24 cm is folded into an open box by cutting a small square from each corner. if the box is to have a maximum volume, what should be the size of the squares cut out?
So let's find the equation of the volume of the box first!
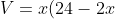^2)
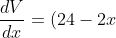^2 + x * -4(24-2x))
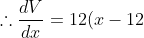(x-4))
For maximum or minimum values,
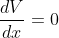
(x-4)=0)
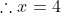 ONLY since
ONLY since  would be too large. If we were to substitute 12 as
would be too large. If we were to substitute 12 as  , we would see we get a length of zero which is not possible.
, we would see we get a length of zero which is not possible.
Taking the second derivative,

Substitute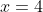 inside.
inside.
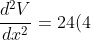 - 192 < 0)
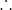 It is maximum and hence the size squares should be 4 cm each to make the volume maximum.
It is maximum and hence the size squares should be 4 cm each to make the volume maximum.
EDIT: Why do you need this in a short amount of time? I thought you were in Year 11.
Second step: To determine the nature of the stationary points, you must do either:
- Take the second derivative. Substitute the x value you just got into the second derivative.
If
If
If
- OR you test points left and right of the first derivative.
The steps above is to see if the value at that coordinate is a maximum or minimum.
[Note: I am assuming you have got the formula before differentiating the function. Also if you take points to the left and right of a value you must take it significantly close to it. (Eg. Testing to the left and right of 5 means substitute values close to it such as 4.9 and 5.1)]
Example question: With reference to this beautiful picture I drew!

A square tin plate of length 24 cm is folded into an open box by cutting a small square from each corner. if the box is to have a maximum volume, what should be the size of the squares cut out?
So let's find the equation of the volume of the box first!
For maximum or minimum values,
Taking the second derivative,
Substitute
EDIT: Why do you need this in a short amount of time? I thought you were in Year 11.
Last edited:
Aysce
Well-Known Member
- Joined
- Jun 24, 2011
- Messages
- 2,393
- Gender
- Male
- HSC
- 2012
Yeah I am in year 11, but my tutor is including it in a massive test with other year 11/12 subjects which is a pain considering I have 10 topics to study, which is utterly ridiculous D:First of all, you must find the first derivative. For stationary points, set the first derivative to zero and find the x-values. Hence substitute into your original equation to find the corresponding y values.
Second step: To determine the nature of the stationary points, you must do either:
- Take the second derivative. Substitute the x value you just got into the second derivative.
If, a maximum turning point occurs.
If, a minimum turning point occurs.
If, a POSSIBLE inflexion point occurs. (In this case you must test to the left and to the right of the value. This will probably NEVER happen if it asks you to find maximum or minimum values.)
- OR you test points left and right of the first derivative.
The steps above is to see if the value at that coordinate is a maximum or minimum.
[Note: I am assuming you have got the formula before differentiating the function. Also if you take points to the left and right of a value you must take it significantly close to it. (Eg. Testing to the left and right of 5 means substitute values close to it such as 4.9 and 5.1)]
Example question: With reference to this beautiful picture I drew!
(http://imageshack.us/f/695/foraysce.jpg/)
A square tin plate of length 24 cm is folded into an open box by cutting a small square from each corner. if the box is to have a maximum volume, what should be the size of the squares cut out?
So let's find the equation of the volume of the box first!
For maximum or minimum values,
ONLY since
would be too large. If we were to substitute 12 as
, we would see we get a length of zero which is not possible.
Taking the second derivative,
Substituteinside.
It is maximum and hence the size squares should be 4 cm each to make the volume maximum.
EDIT: Why do you need this in a sort amount of time? I thought you were in Year 11.
EDIT: Isn't this 3u yr 11 calculus? O.O
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
No. This will be in your 2 Unit HSC.Yeah I am in year 11, but my tutor is including it in a massive test with other year 11/12 subjects which is a pain considering I have 10 topics to study, which is utterly ridiculous D:
EDIT: Isn't this 3u yr 11 calculus? O.O
