Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Can someone explain how to answer this composite function question (1 Viewer)
- Thread starter missuslie
- Start date
cheesynooby
Well-Known Member
i think the best method for these kinds of questions is usually to just sub values in (almost always works, less room for mistakes)
but heres a perhaps less guess and check type approach
B is gone because of the change in gradient over a range that does not match the range of h(x) (if it was B we should see peaks lower in h(x))
(also B just looks pretty asymmetrical and ew)
we expect a peak at x = -1/2 (if wlog we let each tick mark be 1 unit)
that means the blue graph at x = -1/2 should be positive --> leading to a positive h(x) value since the f(x) is positive for positive inputs
so the only graph that satisfies this is C.
A and D would be the same graph but with a different phase since f(x) is the same and g(x) is only shifted horizontally (so basically we only have one option anyway: to test points)
but heres a perhaps less guess and check type approach
B is gone because of the change in gradient over a range that does not match the range of h(x) (if it was B we should see peaks lower in h(x))
(also B just looks pretty asymmetrical and ew)
we expect a peak at x = -1/2 (if wlog we let each tick mark be 1 unit)
that means the blue graph at x = -1/2 should be positive --> leading to a positive h(x) value since the f(x) is positive for positive inputs
so the only graph that satisfies this is C.
A and D would be the same graph but with a different phase since f(x) is the same and g(x) is only shifted horizontally (so basically we only have one option anyway: to test points)
cheesynooby
Well-Known Member
(ok i feel like i didnt stress this enough but for these questions just save urself the hassle and test points/do a table of values it's just more efficient)
coolcat6778
Вanned
- Joined
- Jun 9, 2024
- Messages
- 1,919
- Gender
- Female
- HSC
- 2025
or just skip it completely. make an educated guess. mcq are designed like this to test ur elimination skills
coolcat6778
Вanned
- Joined
- Jun 9, 2024
- Messages
- 1,919
- Gender
- Female
- HSC
- 2025
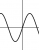
you can see the function is ODD,
g(x) must be ODD as well since g(x) is the inside function
hence C
g(x) must be ODD as well since g(x) is the inside function
hence C
cheesynooby
Well-Known Member
oh wait thats smartyou can see the function is ODD,
g(x) must be ODD as well
hence C
coolcat6778
Вanned
- Joined
- Jun 9, 2024
- Messages
- 1,919
- Gender
- Female
- HSC
- 2025
for another question like this, check Math advanced 2020
lazystudentzzz
Active Member
- Joined
- Feb 2, 2025
- Messages
- 104
- Gender
- Female
- HSC
- 2025
how do we tell from graphs if a function is odd or even? its just ab symmetry right?you can see the function is ODD,
g(x) must be ODD as well since g(x) is the inside function
hence C
symmetrical (reflected on y-axis) = even function
point symmetry (rotated on a point) = odd function
coolcat6778
Вanned
- Joined
- Jun 9, 2024
- Messages
- 1,919
- Gender
- Female
- HSC
- 2025
Odd means the graph passes through the origin from bottom left to top right quadrant OR top left to bottom right. (which is symmetry)
Even just means it's symmetrical in the y axis
Even just means it's symmetrical in the y axis
Attachments
-
5.8 KB Views: 9
lazystudentzzz
Active Member
- Joined
- Feb 2, 2025
- Messages
- 104
- Gender
- Female
- HSC
- 2025
tysm!Odd means the graph passes through the origin from bottom left to top right quadrant OR top left to bottom right. (which is symmetry)
Even just means it's symmetrical in the y axis
odd ∘ odd = odd: The composition of two odd functions is odd.
even ∘ odd = even: The composition of an even function and an odd function is even.
odd ∘ even = even: The composition of an odd function and an even function is also even.
Any function composed with an even function is even.
The graph of h(x)is odd. So both f(x) and g(x) must be odd. option C is the only one satisfying this condition.
even ∘ odd = even: The composition of an even function and an odd function is even.
odd ∘ even = even: The composition of an odd function and an even function is also even.
Any function composed with an even function is even.
The graph of h(x)is odd. So both f(x) and g(x) must be odd. option C is the only one satisfying this condition.
Since we know h(-x) = -h(x), we can say h(-x) = f(g(-x)) and -h(x) = -f(g(x)). So we can tell that f(g(-x)) = -f(g(x)). Now we can ask ourselves what if g(x) is odd or even. If it's odd g(-x) = -g(x) then f(-g(x)) = -f(g(x)) which indicates that f is odd too and if g is even then f(g(x)) = -f(g(x)) which would require f(g(x)) = 0 for all x in the domain. Hence, we can say that g(x) should be odd as well as f(x).