-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Difficult complex geometry q (1 Viewer)
- Thread starter =)(=
- Start date
Can you show us what you tried first for part ii. Just give it go.View attachment 35292
part ii please
Did the sample solution not help?I am pretty lost for ii for some reason visually the modulus looks like R but it cant be
I would recommend finding the modulus and the argument separately.
For the modulus you would use pythag
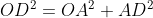 Given that since OB is a tangent to the circle
Given that since OB is a tangent to the circle
+(R-r)^2}\ \text{pythag again as}\ CO^2=CA^2+OA^2\\OD=\sqrt{(R^2-r^2)+(R-r)^2}\\OD=\sqrt{R^2-r^2+R^2-2Rr+r^2}\\OD=\sqrt{2R^2-2Rr}) Which is the modulus of D
Which is the modulus of D
Now to find the argument, we have to use the triangle COD which is a Isosceles triangle cause CO=CD as they are both the radius of the same circle.
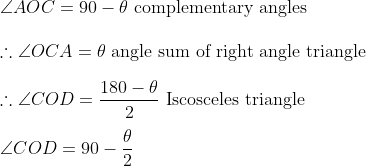
Therefore the angle between line OD and the positive real axis would be cause it is complementary to
cause it is complementary to 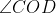
Hence the complex number represented by D would be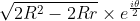
For the modulus you would use pythag
Now to find the argument, we have to use the triangle COD which is a Isosceles triangle cause CO=CD as they are both the radius of the same circle.
Therefore the angle between line OD and the positive real axis would be
Hence the complex number represented by D would be

