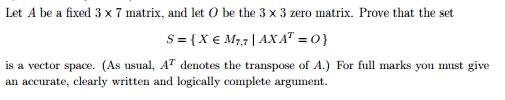leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Re: MATH1231/1241/1251 SOS Thread
In that case, how could you prove this then?
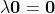
As a reference, they proved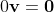 like this
like this
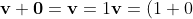\textbf{v}=1\textbf{v}+0\textbf{v}=\textbf{v}+0 \textbf{v}\\ \text{Then by cancellation property }0\textbf{v}=\textbf{0})
Also gonna take a stab at the axioms they used...
1. Existence of 0
2. Scaling factor of 1
3. arithmetic (or just existence of 0 in field of scalars)
4. Scalar distributive law
5. Scaling factor of 1
For some reason I kept thinking what was the problem with doing it component wise...What other method do you have in mind? (Induction helps takes care of it nicely if you want to prove it straight from the axioms.)
$)
In that case, how could you prove this then?
As a reference, they proved
Also gonna take a stab at the axioms they used...
1. Existence of 0
2. Scaling factor of 1
3. arithmetic (or just existence of 0 in field of scalars)
4. Scalar distributive law
5. Scaling factor of 1
Last edited: