asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
It may be from 3U Fitzpatrick but I'm not sure
A rectangular vessel is divided into 2 equal compartments by a vertical porous membrane. Liquid in one compartment, initially at a depth of 20cm, passes into the other compartment, initially empty, at a rate proportional to the difference in the levels.
a) If the depth of liquid in one of the vessels at any time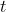 is
is  , show that
, show that 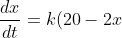)
b) Show that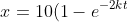)
c) If the level in the originally empty compartment rises 2cm in the first 5 minutes, after what time difference will the difference in the levels be 2cm?
Please help with c).
Thankyou!
A rectangular vessel is divided into 2 equal compartments by a vertical porous membrane. Liquid in one compartment, initially at a depth of 20cm, passes into the other compartment, initially empty, at a rate proportional to the difference in the levels.
a) If the depth of liquid in one of the vessels at any time
b) Show that
c) If the level in the originally empty compartment rises 2cm in the first 5 minutes, after what time difference will the difference in the levels be 2cm?
Please help with c).
Thankyou!
