MC Squidge
BOS' Apex Predator
i) The complex numbers 2+1, -1-2i and z represent points A, B and C on the Argand Diagram. Find One Possible value of z such that Triangle ABC is right angled at C and |CB|=2|CA|
ii)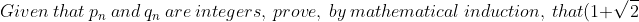^n=p_n+q_n\sqrt{2}\ for\ all\ positive\ integers\ n)
iii) Given x^2-y^2+xy=5
a)find dy/dx and hence points on the curve whose tangents are vertical or horizontal
b) Discuss the behaviour of the curve for large values of x
c) Sketch the curve
ii)
iii) Given x^2-y^2+xy=5
a)find dy/dx and hence points on the curve whose tangents are vertical or horizontal
b) Discuss the behaviour of the curve for large values of x
c) Sketch the curve
Last edited:
