-
Want to help us with this year's BoS Trials? Let us know before 30 June. See this thread for details -
Looking for HSC notes and resources? Check out our Notes & Resources page
How do I solve this inequality? (1 Viewer)
- Thread starter Bob_man
- Start date
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 562
- Gender
- Male
- HSC
- 2018
Okay, are you doing Maths extension II? If you do so or not note that the absolute values represent the length of distance from 0 to a certain equation so in this case,
what we have here is that the value has to be either bigger than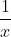 or smaller than
or smaller than 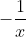 . With that knowledge in hand, the next step is to state that where is
. With that knowledge in hand, the next step is to state that where is 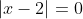 because this is the point where the line reflects itself off a wall.
because this is the point where the line reflects itself off a wall.
Do you see it?
If so congrats because that serves a vital role in what we are doing the reason is that when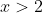
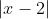 is just simply when is
is just simply when is 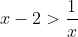 and when
and when 
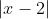 is simply when is
is simply when is 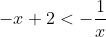 .
.
Now what I am about to do will attract sceptics but hey the reason why it works will be revealed in a while.
To start off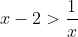 . Now meet the critics. "Sir, why are you allowed to say that
. Now meet the critics. "Sir, why are you allowed to say that 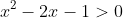 when normally our maths teacher always tells us to multiply by an even power before doing this?"
when normally our maths teacher always tells us to multiply by an even power before doing this?"
The reason is that at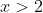 all the values that come after it are positive as thus, it is safe to multiply by x because multiplying by a positive value does not change the result in a fraction. The next step is to find the roots in
all the values that come after it are positive as thus, it is safe to multiply by x because multiplying by a positive value does not change the result in a fraction. The next step is to find the roots in 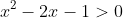 . If you have found the roots a little challenge awaits you find the root that is greater than 2. If you have done than Horray you are halfway done.
. If you have found the roots a little challenge awaits you find the root that is greater than 2. If you have done than Horray you are halfway done.
The next step is this find where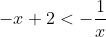 . The next step wiill be
. The next step wiill be 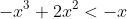 . Bring everything to one side and it becomes
. Bring everything to one side and it becomes  < 0) have a look at this
have a look at this  > 0) when we went from
when we went from  < 0) to
to  > 0) is simply
is simply 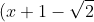(x+1+\sqrt{2})) . The rest is history. There you can find the values that satisfy
. The rest is history. There you can find the values that satisfy 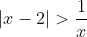 . If you had to do this question by hand my method will work.
. If you had to do this question by hand my method will work.
what we have here is that the value has to be either bigger than
Do you see it?
If so congrats because that serves a vital role in what we are doing the reason is that when
Now what I am about to do will attract sceptics but hey the reason why it works will be revealed in a while.
To start off
The reason is that at
The next step is this find where
Last edited:
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 562
- Gender
- Male
- HSC
- 2018
The absolute value plays an important role.Just clearing some things up so x>2 since the inequality wouldn't work otherwise? And from that you got x^2-2x-1>0 which you solved by completing the square giving x>1 ± √ 2 and since x is positive it is 1+ √ 2?
Last edited:
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 562
- Gender
- Male
- HSC
- 2018
View attachment 34513
hope that helps
Have a look at your graph and also the part where I gotOkay, are you doing Maths extension II? If you do so or not note that the absolute values represent the length of distance from 0 to a certain equation so in this case,
what we have here is that the value has to be either bigger thanor smaller than
. With that knowledge in hand, the next step is to state that where is
because this is the point where the line reflects itself off a wall.
Do you see it?
If so congrats because that serves a vital role in what we are doing the reason is that when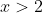
is just simply when is
and when

is simply when is
.
Now what I am about to do will attract sceptics but hey the reason why it works will be revealed in a while.
To start off. Now meet the critics. "Sir, why are you allowed to say that
when normally our maths teacher always tells us to multiply by an even power before doing this?"
The reason is that atall the values that come after it are positive as thus, it is safe to multiply by x because multiplying by a positive value does not change the result in a fraction. The next step is to find the roots in
. If you have found the roots a little challenge awaits you find the root that is greater than 2. If you have done than Horray you are halfway done.
The next step is this find where. The next step will be
. Bring everything to one side and it becomes
have a look at this
is simply
. The rest is history. There you can find the values that satisfy
. If you had to do this question by hand my method will work.
so does that mean x>1+√ 2 is the answer?Have a look at your graph and also the part where I got. There you can focus on all the values of x that give a positive value
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 562
- Gender
- Male
- HSC
- 2018
One of them but also note there is another solution. Notice when I said the absolute values it means that you can haveso does that mean x>1+√ 2 is the answer?
Two conditions provided.
Apologies for not clarifying correctly and I wish you a Merry Christmas.


