-
Best of luck to the class of 2024 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
HSC 2016 MX2 Marathon ADVANCED (archive) (3 Viewers)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
Re: HSC 2016 4U Marathon - Advanced Level
I remember the 2014 HSC 4U Advanced marathon was allowed to continue for a couple of years. Why not the 2015 one (or why did the 2014 one have to stop)? (Though the 2015 one probably wasn't as good or vibrant as the 2014 one, so it wouldn't be as fun to keep it going I suppose.)Post questions within the scope of Mathematics Extension 2 that are in general Q16 and beyond, focusing on problem solving and neat results within the reach of elementary mathematics.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2016 4U Marathon - Advanced Level
2014 (actually 2013) stopped because mods wanted it to (I wanted it to keep going)I remember the 2014 HSC 4U Advanced marathon was allowed to continue for a couple of years. Why not the 2015 one (or why did the 2014 one have to stop)? (Though the 2015 one probably wasn't as good or vibrant as the 2014 one, so it wouldn't be as fun to keep it going I suppose.)
Re: HSC 2016 4U Marathon - Advanced Level
(They do need to be positive integers of course (for that to be true).)
Re: HSC 2016 4U Marathon - Advanced Level
Haha yeah, it was from 2013. And started in calendar year 2012 I think.2014 (actually 2013) stopped because mods wanted it to (I wanted it to keep going)
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,650
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2016 4U Marathon - Advanced Level
Here's a crappy one I made
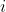 $ Prove that the equation $ 16x^4 -16x^2 +1 $ has a root $ x=\frac{1}{2}\sqrt{2-\sqrt{3}} $ by letting $ x= \frac{1}{2}\sqrt{2-\sqrt{3}} )
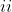 $ Using De Moivre's theorem find the quartic equation with a root $ cos(\frac{5 \pi}{12}) )
 $ Explain the significance of the results found above. $ )
Here's a crappy one I made
Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon - Advanced Level
}.)

 Evaluate the volume of the resulting solid.$)
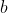 Evaluate the surface area of the resulting solid.$)
 Compare the results obtained from a) and b). Explain the significance of these results.$)
Last edited:
Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon - Advanced Level
I'm guessing the geometric interpretation is that if you subtract w from z, it will be 'longer' (larger modulus) or be equal to the length of subracting the modulus of w from the modulus from z. Though that was a complete guess.
Small error: http://m.imgur.com/glJoL07
Proof: http://m.imgur.com/QApReFiSince 2016'ers probably have just started complex numbers recently, relatively easy Q to start off:

I'm guessing the geometric interpretation is that if you subtract w from z, it will be 'longer' (larger modulus) or be equal to the length of subracting the modulus of w from the modulus from z. Though that was a complete guess.
Small error: http://m.imgur.com/glJoL07
Last edited:
DatAtarLyfe
Booty Connoisseur
- Joined
- Mar 10, 2015
- Messages
- 1,805
- Gender
- Female
- HSC
- 2016
Re: HSC 2016 4U Marathon - Advanced Level
Oh cool theres a 4u section now for us. Now i have something to do when i'm bored
Oh cool theres a 4u section now for us. Now i have something to do when i'm bored
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,650
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2016 4U Marathon - Advanced Level
I think I'll recruit some of the new year 12s in my school to this forum.
I think I'll recruit some of the new year 12s in my school to this forum.
Re: HSC 2016 4U Marathon - Advanced Level
, the distance between the two points (which is $|z-w|$) is at least the width of the annulus formed by the two concentric circles (which is $\Big{|} |z|-|w|\Big{|}$, i.e. the difference of the radii).$)
Proof: http://m.imgur.com/QApReFi
I'm guessing the geometric interpretation is that if you subtract w from z, it will be 'longer' (larger modulus) or be equal to the length of subracting the modulus of w from the modulus from z. Though that was a complete guess.
Small error: http://m.imgur.com/glJoL07
dan964
what
Re: HSC 2016 4U Marathon - Advanced Level
It can simply be geometrically proved by using the triangle inequalities of the points O (origin), Z and W
|w|+|z-w|>= |z|
and |z|+|z-w|>= |w|
Rearranging gives
|z-w|>= |z|-|w|
and |z-w| >= |w|-|z|
which can leads to the generalised result:
|z-w|>= ||z|-|w||
Or in other terms the minimum distance between one point Z and another X on the two concentric circles i.e. |z-w| is the distance between the concentric circles itself ||z|-|w||. Equality occurs when arg z = arg w (it is a pointless statement if either z or w is 0)
It can simply be geometrically proved by using the triangle inequalities of the points O (origin), Z and W
|w|+|z-w|>= |z|
and |z|+|z-w|>= |w|
Rearranging gives
|z-w|>= |z|-|w|
and |z-w| >= |w|-|z|
which can leads to the generalised result:
|z-w|>= ||z|-|w||
Last edited:
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,650
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2016 4U Marathon - Advanced Level
.Here's a crappy one I made
 $ Explain the significance of the results found above. $ )
Re: HSC 2016 4U Marathon - Advanced Level
What do you mean by using Demoivres theorem? It's not exactly clear what you're asking for, unless you mean like use the demoivre's theorem to derive the double angle formula for cos, and use that to find the exact value of cos (5pi/12), which is the squared value of the expression in part 1
Zen2613
Member
Re: HSC 2016 4U Marathon - Advanced Level
I think he wants us to use demoivre to find an expression for cos(4theta) in terms of cos(theta) because that will be a quartic which will probably resemble his 16x^4 - 16x^2 -1 = 0 thingo.What do you mean by using Demoivres theorem? It's not exactly clear what you're asking for, unless you mean like use the demoivre's theorem to derive the double angle formula for cos, and use that to find the exact value of cos (5pi/12), which is the squared value of the expression in part 1
Zen2613
Member
Re: HSC 2016 4U Marathon - Advanced Level
I like that one. Nice introduction to 4 unit problems. But since you made the problem, how did you actually find the roots for that quartic equation in x ? The 1/2sqrt(2-sqrt(3)) ones.
I like that one. Nice introduction to 4 unit problems. But since you made the problem, how did you actually find the roots for that quartic equation in x ? The 1/2sqrt(2-sqrt(3)) ones.
- Status
- Not open for further replies.

