HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,547
- Gender
- Male
- HSC
- 2013
Prove by mathematical induction that: 2^n > 3n^2 for n is greater or equal to 8
n=8, true
n=k,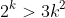
n=k+1, 2^(k+1) > 3(K+1)^2
DAMN forgot to copy from latex
LHS = 2.2^k
>6k^2
= 3k^2 + 6k + 3 + 3k^2 - 6k - 3
=3(k+1)^2 + 3k^2 - 6k - 3
All i need to do is to prove that 3k^2 - 6k - 3 >0
Attempt 1
sub in k = 8, and its >0
Attempt 2
n>8
k>8 (assumption)
k^2 >64
3k^2 > 192
6k>48
so 3k^2 - 3k > 144
so 3k^2 - 3k - 3 >0
This is very messy.... can anyone enlighten me or tell me a neater proof
n=8, true
n=k,
n=k+1, 2^(k+1) > 3(K+1)^2
DAMN forgot to copy from latex
LHS = 2.2^k
>6k^2
= 3k^2 + 6k + 3 + 3k^2 - 6k - 3
=3(k+1)^2 + 3k^2 - 6k - 3
All i need to do is to prove that 3k^2 - 6k - 3 >0
Attempt 1
sub in k = 8, and its >0
Attempt 2
n>8
k>8 (assumption)
k^2 >64
3k^2 > 192
6k>48
so 3k^2 - 3k > 144
so 3k^2 - 3k - 3 >0
This is very messy.... can anyone enlighten me or tell me a neater proof
Last edited:
