Q12 pls
Attachments
-
2.6 MB Views: 28
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Note: The induction procedure is different for every person so I'm just going to focus on the solution itself, ask your teacher for how they'd like it when you start year 11.Q12 pls

ohh makes sense now, I also had another question to do with induction with inequalities, I saw this step in one worked example somewhere was the 1+1/2k able to be discarded as since k>1 removing the expression just makes the rhs of a lesser value?Note: The induction procedure is different for every person so I'm just going to focus on the solution itself, ask your teacher for how they'd like it when you start year 11.
[Base Case]
When there is 3 sides, you will form a triangle and this has no diagonals.
Hence, n = 3 is a true statement.
[Induction Hypothesis]
Suppose k is an integer and true for n >= 3.
n = k;
Polygon with k sides will havediagonals
[Proving stage]
n = k + 1;
Claim/Proof: We have to prove a k+1 side polygon hasdiagonals
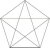
From induction hypothesis, a polygon with k sides will havediagonals. When adding an extra side, the new vertex will form k - 2 diagonals with other vertexes ignoring those adjacent to it. As the new side is added, it also creates an extra diagonal from the previous vertex point with the first vertex point (please draw cases for n =4,5,6 to understand). This is unaccounted when considering the diagonals only formed from the new vertex.
Here are some really shoddy diagrams to give an idea of what I'm talking about. The red diagonal (please ignore the fact the diagonal's not straight) is the diagonal thats unaccounted for from going from n = 5 to n = 6 (you can consider this as k = 5) and the yellow vertex is the new vertex. You can see k - 2 ( 6 - 2 = 4) diagonals are formed solely from the diagonals however the edges are not considered.
View attachment 34655 View attachment 34654
n = 5 to n = 6.
This the logic we're using for n = k + 1.
...
Hence proven by principles of mathematical induction for n>=3 yadda yadda this part is whatever your teacher wants etc.
For these type of qs, I would just try to draw diagrams for the cases and if you still don't get the pattern, draw for more cases and it'll become apparent (as above for n = 5 to n = 6) and then proceed. I think there's similar type qs like proving by induction that n lines divding the plane into certain amount regions or smthn like that.

Yeah pretty much, the value ofohh makes sense now, I also had another question to do with induction with inequalities, I saw this step in one worked example somewhere was the 1+1/2k able to be discarded as since k>1 removing the expression just makes the rhs of a lesser value?View attachment 34659
You were really close.Soz got another one, for part a i get (a^n-b^n)(a-b) greater than or equal to 0 but im lost from thereView attachment 34660
ohhhh okay thank youYou were really close.
(a-b)\geq{0}\\\\a^n\cdot{a}-a^nb-b^na+b^n\cdot{b}\geq{0}\\\\a^{n+1}+b^{n+1}\geq{a^nb+b^na})
