Interesting problem (1 Viewer)

seanieg89 · Sep 20, 2017

Here is an interesting problem. If you are not comfortable with higher dimensional spaces, replace "affine hyperplane" with "line" (not necessarily through the origin), and fix n=2 in the below.

Suppose we have finitely many affine hyperplanes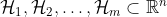 $\mathcal{H}_1,\mathcal{H}_2,\ldots,\mathcal{H}_m \subset \mathbb{R}^n$
and suppose a point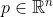 $p\in\mathbb{R}^n$ is chosen arbitrarily.

Prove that any sequence defined by:

$x_0=p$
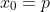
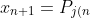$x_{n+1}=P_{j(n)}(x_n)$

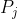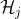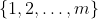is bounded, where $P_j$ denotes orthogonal projection onto $\mathcal{H}_j$ and the sequence $j(n)$ in $\{1,2,\ldots,m\}$ is chosen arbitrarily.

Is your bound independent of your choice of sequence $j(n)$ ?

Interesting problem (1 Viewer)

seanieg89

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 1)