47. Largely depends on what you have learned / what definition of determinant you are working from.
Since you are just talking about square row echelon matrices (which are necessarily upper triangular), you can probably just use the fact that the determinant of an upper triangular square matrix is just the product of diagonal entries. (You could easily prove this fact inductively or otherwise if you like.)
Also if you multiply out two upper triangular square matrices, a simple computation shows that the resulting matrix is also upper triangular, and the diagonal entries are the product of the corresponding diagonal entries of the factor matrices.
This fact makes the result trivial.
48. Determinants are preserved under taking transpose, so
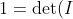=\det(QQ^T)=\det(Q)\det(Q^T)=\det(Q)^2.)