seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
The theorem of Pappus is a useful tool for quickly calculating volumes (and surface areas) of solids of revolution.
It states that if we obtain a solid of revolution by rotating a region of area A about a line l, then the resultant volume will be Ad, where d is the distance traced out by the centroid of our region as we rotate.
For example, a torus (donut) can be obtained by rotating a circle of radius r about a line l, which is R units away from the centre of this circle. By the theorem of Pappus, such a solid will have volume:
Whilst it cannot be used without proof in an MX2 exam, the proof of a special case of it is good practise for the Volumes topic.
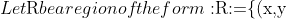:a\leq x\leq b, g(x)\leq y \leq f(x)\}$ where $f$ and $g$ are continuous functions on the interval $a\leq x \leq b$ with $g< f$. The \emph{centroid} of such a region has $x$-coordinate:\\ $x_c= \frac{\int_a^b x(f(x)-g(x))\, dx}{\int_a^b f(x)-g(x)\, dx}.$ Prove the theorem of Pappus for the solids of revolution which we can obtain by rotating R about a vertical line in the plane. $)
Edit:
Ignore the title, the discussion of moments is beyond MX2 so you will have to take the centroid formula on faith! For geometrically simple 2d regions, there are much easier ways to calculate a centroid.
It states that if we obtain a solid of revolution by rotating a region of area A about a line l, then the resultant volume will be Ad, where d is the distance traced out by the centroid of our region as we rotate.
For example, a torus (donut) can be obtained by rotating a circle of radius r about a line l, which is R units away from the centre of this circle. By the theorem of Pappus, such a solid will have volume:
Whilst it cannot be used without proof in an MX2 exam, the proof of a special case of it is good practise for the Volumes topic.
Edit:
Ignore the title, the discussion of moments is beyond MX2 so you will have to take the centroid formula on faith! For geometrically simple 2d regions, there are much easier ways to calculate a centroid.
Last edited:
