Run hard@thehsc
Well-Known Member
- Joined
- Oct 7, 2021
- Messages
- 784
- Gender
- Male
- HSC
- 2022
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
View attachment 34434
I did part 2 but I need help to confirm weather my method was correct... can someone show how this problem can be approached??
I understand this but can u please expand on how dividing z^5-1 with z-1 gets the rhs? Thanks!has roots
letbe w,
be w conjugate and j for the other root etc.
dividing z^5 -1 with z -1 gets the RHS
same with the j root.
and then you get the result as required.
edit: don't know how to do conjugates so if anyone reading could show how to latex it i would appreciate
You can prove it through polynomial division. If you were to manually divide both polynomials, you would get that term.I understand this but can u please expand on how dividing z^5-1 with z-1 gets the rhs? Thanks!
Ahhhhh okkk makes sense now thank you!!You can prove it through polynomial division. If you were to manually divide both polynomials, you would get that term.
Or
You could factorise z^5 - 1 into two polynomials
as you can see, all the terms in the polynomial are multiplied by z first, and then the regular polynomial is multiplied by -1 so all the terms between z^5 and -1 would be cancelled out
which is
so when you divide by z - 1.
(z^4+z^3+z^2+1)}{z-1} = (z^4+z^3+z^2+1) )
Note there is a typo there can you spot his mistake.Ahhhhh okkk makes sense now thank you!!
You can use \bar{z} to getedit: don't know how to do conjugates so if anyone reading could show how to latex it i would appreciate
An easy way to establish thatI understand this but can u please expand on how dividing z^5-1 with z-1 gets the rhs? Thanks!
You can use \bar{z} to getbut I prefer \overline{} so I can get \overline{z} is
and \overline{a+ib} is
because \bar{a+ib}, giving
looks ridiculous.
Yep when I was copying pasting the roots, I must've forgotten to change the 2pi to 4pi. Thanks for that.@5uckerberg was it his roots. One his roots were supposed to be e^i(-4pi/5) I believe.... @ExtremelyBoredUser thanks btw!
Well he has changed it.@5uckerberg was it his roots. One his roots were supposed to be e^i(-4pi/5) I believe.... @ExtremelyBoredUser thanks btw!
Not the solution to (v) but just another method for these type of questions;How would you do part 5 of this question? I have done questions like these before, but somehow can't find the method I used before. Thanks!
View attachment 34431
and
Can be found without complex numbers:
Yeah that's true, I was trying to use part ii cause the question asked to.The two results that you have derived:
and
Can be found without complex numbers:
and then set firstand then
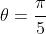
I understand... I was wondering whether it meant to use part (iv), or about noting that part(iv) was derived from (ii), and so using it is building from part (ii)Yeah that's true, I was trying to use part ii cause the question asked to.
I think the question would have explicitly stated to use part (iv) if they meant for you to use it. But it I guess the question was kinda building up to that point through all the previous parts, so your way would have been correct too and in timed conditions my method would take way to long for 2 marks.I understand... I was wondering whether it meant to use part (iv), or about noting that part(iv) was derived from (ii), and so using it is building from part (ii)
