Woah, thanks again Integrand!


Another question (I never seem to run out, huh? haha) how would you find range if you knew max height, but not theta? (theta being the angle in ucos(theta) and usin(theta)) U= 8m/s and g= 10 m/s^-2 . Is g always -10?
"A long-jumper running at 8m/s jumps into the air, rising to a height of 0.6m. What is the length of his jump assuming g= 10ms^-2?"
Ans: 5.00m
g is the local acceleration due to gravity. On Earth,
g is about 9.8 m s
-2, which is approximately 10 m s
-2. If you're asked to calculate something numerically and the question doesn't tell you what to use for
g, use either 9.8 or 10 (10 would be easier to work with), and say what value for
g you're using.
Here's how to do the question you posted.
Let the angle of the jumper's jump with the ground be
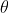
. We don't know what this is yet, but it's some constant value between 0 and 90 degrees which we will be able to find using the given info. The initial jump speed was 8 m s
-1, so the
x and
y components of the initial speed are

and

respectively.
Now, set up your usual equations of motion (I assume you know how to do these), the relevant ones will be:
t \text{ }(1))
)
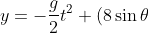t \text{ }(3))
.
Now we're given that the max. height is 0.6 m. Max. height occurs when

is 0 (e.g. when you throw a ball in the air, when it reaches its maximum height, it just stops moving in the vertical direction). But

when

.
So at this time,
y = 0.6, i.e.
^2+(8\sin \theta)\cdot\frac{8\sin\theta}{g}=0.6 )
(from Eqn. 3)


.
So

. Now we've found

(previously an unknown) in terms of known values.
Now, at this time,
x is half the range, since when the max. height is reached, you're at half the range, by symmetry of a parabola.
At this time, from Eqn. 1,

(since
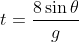
).
But

, so at this time,
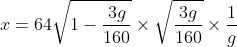
.
This is half the range, so the full range is double this, i.e.
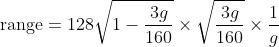
.
Plug in
g = 10 m s
-2, and you'll get the range to be 4.995998399....m, or 5.00 m to 3 sig. fig.
