leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Was helping out a friend with it but for the last part, I was wondering if there was a shorter method?
Q:
You have the hyperbola xy=16
a) Sketch + indicate where the hyperbola intersects its axes of symmetry
So (±4,±4)
b) Consider P(4p,4/p), Q(4q,4/q) where p,q>0
Then the chord PQ has equation x+pqy=4(p+q)
c) The tangent at P is x+p2y=8p
d) The tangents at P and Q intersect at T, whose coordinates are ( 8pq/(p+q), 8/(p+q) )
e) The chord passes through N(0,8) -> brings up the condition 2pq=p+q
The locus of T is the line x=4, where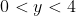
For the part in finding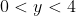
I did it a bit too tediously (in my opinion). I firstly rewrote the y-coordinate as y=4/(pq), and I said obviously y>0 given p,q>0
But then I rearranged 2pq=p+q to give q=p/(2p-1)
Thus y=4(2p-1)/p2 and I went on saying that calculus (i.e. stationary points etc) can be used to show that a global maximum occurs at y=4. Hence we disregard y=4 as that implies p=q (if so, T is not strictly defined) to get 0<y<4
Dilemma: Any possible way to avoid the calculus proof to get the upper bound on y?
Q:
You have the hyperbola xy=16
a) Sketch + indicate where the hyperbola intersects its axes of symmetry
So (±4,±4)
b) Consider P(4p,4/p), Q(4q,4/q) where p,q>0
Then the chord PQ has equation x+pqy=4(p+q)
c) The tangent at P is x+p2y=8p
d) The tangents at P and Q intersect at T, whose coordinates are ( 8pq/(p+q), 8/(p+q) )
e) The chord passes through N(0,8) -> brings up the condition 2pq=p+q
The locus of T is the line x=4, where
For the part in finding
But then I rearranged 2pq=p+q to give q=p/(2p-1)
Thus y=4(2p-1)/p2 and I went on saying that calculus (i.e. stationary points etc) can be used to show that a global maximum occurs at y=4. Hence we disregard y=4 as that implies p=q (if so, T is not strictly defined) to get 0<y<4
Dilemma: Any possible way to avoid the calculus proof to get the upper bound on y?
