Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Find the value of the sum:
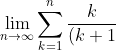!})
Assuming the behaviour of the summands is consistent over large n.
Assuming the behaviour of the summands is consistent over large n.
