Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
I found the taylor series
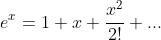

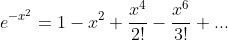
^k}{k!(2k+1)}} +C )
Did i integrate it or not ?
Did i integrate it or not ?
Last edited:
