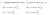The first thing to note with an MCQ like this one is that you don't actually
need to find a general form.
The second is that there can be more than one general form.
Now, the equation here is
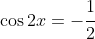
. This has a related angle (acute) given by
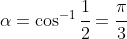
.
The solutions are in the 2nd and third quadrants the cosine function is negative. So, we have:
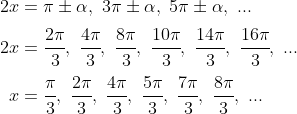
We can now choose the correct answer by looking at which option generates the same set of solutions:
(A)
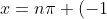^n\cfrac{\pi}{3} \qquad \qquad \text{which generates solutions} \quad x = \cfrac{\pi}{3},\ \cfrac{2\pi}{3},\ \cfrac{7\pi}{3},\ \cfrac{8\pi}{3},\ \cfrac{13\pi}{3},\ \cfrac{14\pi}{3},\ ...)
(B)
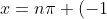^n\cfrac{\pi}{6} \qquad \qquad \text{which generates solutions} \quad x = \cfrac{\pi}{6},\ \cfrac{5\pi}{6},\ \cfrac{13\pi}{6},\ \cfrac{17\pi}{6},\ \cfrac{25\pi}{6},\ \cfrac{29\pi}{6},\ ...)
(C)
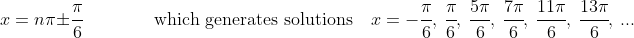
(D)
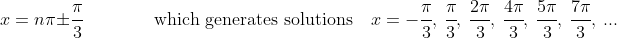
And the answer is clearly (D).
We could have short cut this by looking at our solution set, which includes only multiples of

that appear in all four quadrants and then recognise that (A) and (B) will give solutions only in quadrants 1 and 2, and (C) will give multiples of

.
Having said all that, we can also find the general formula, in which case your key mistake is not realising that the related angle must be acute whether the function is positive or negative, and you adjust for quadrants from there.
In other words, we seek
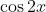
with a related angle
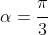
, but in quadrants 2 and 3 (as cos is negative). In other words:
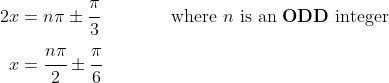
This is why there are the options with

in them...
Anyway, if

is ODD, then I can set
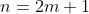
where

is any integer:
\pi}{2} \pm \cfrac{\pi}{6} \\ x &= \left(\cfrac{2m\pi}{2} + \cfrac{\pi}{2}\right) \pm \cfrac{\pi}{6} \\ x &= m\pi + \cfrac{\pi}{2} \pm \cfrac{\pi}{6} \\ x &= m\pi + \cfrac{\pi}{2}\left(1 \pm \cfrac{1}{3}\right) \\ x &= m\pi + \cfrac{\pi}{2}\left(\cfrac{3 \pm 1}{3}\right) \\ x &= m\pi + \cfrac{\pi}{2} \times \cfrac{3 - 1}{3} \qquad \text{or} \qquad x = m\pi + \cfrac{\pi}{2} \times \cfrac{3 + 1}{3} \\ x &= m\pi + \cfrac{\pi}{2} \times \cfrac{2}{3} \qquad \text{or} \qquad x = m\pi + \cfrac{\pi}{2} \times \cfrac{4}{3} \\ x &= m\pi + \cfrac{\pi}{3} \qquad \text{or} \qquad x = m\pi + \cfrac{2\pi}{3} \\ x &= m\pi + \cfrac{\pi}{3} \qquad \text{or} \qquad x = m\pi + \pi - \cfrac{\pi}{3} \\ x &= m\pi + \cfrac{\pi}{3} \qquad \text{or} \qquad x = (m + 1)\pi - \cfrac{\pi}{3} \end{align*})
Now, since

takes the value of every integer, and so therefore does
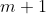
, I can combine these and generate the same solutions, though in a different order, as

, which is the answer given in the question. However, if an exam question sought a general formula, I think that
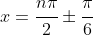
is fine,
so long as you clearly state the requirement that  is ODD.
is ODD. In the alternative, I also think that
\pi}{2} \pm \cfrac{\pi}{6})
for all integers

is a reasonable answer.