Consider two polynomials P(x) and F(x)
When P(x) is divided by
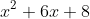
the remainder is 2x-11
When F(x) is divided by
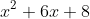
the remainder is x+4
With each division the quotient is the same.
(i) Show that P(x) and F(x) much have the same degree.
For (i), the key is that the
quotients of both of P(x) and F(x) when divided by the same divisor are the same.
ANY polynomial divided by a quadratic MUST have a linear remainder in the form ax + b (note that the remainder can be constant if a = 0), so the remainder expression itself is somewhat irrelevant in this part.
So: (note the Q(x) expression is identical in both equations)
P(x) = (x² + 6x + 8)Q(x) + 2x - 11
F(x) = (x² + 6x + 8)Q(x) + x + 4
Let p be the degree of Q(x), so the degree of P(x) is (p + 2) and the degree of F(x) is (p + 2) as well, because multiplication of a polynomial of degree a with a polynomial of degree b, gives a polynomial of degree a + b.
To see this a bit more rigorously let the quotient be a general polynomial of degree p:
Q(x) = a
px
p + a
p - 1x
p - 1 + .... + a
2x
2 + a
1x + a
0
We then get:
(x² + 6x + 8)(a
px
p + a
p - 1x
p - 1 + .... + a
2x
2 + a
1x + a
0)
= (a
px
p+2 + a
p - 1x
p + 1 + .... + a
2x
4 + a
1x
3 + a
0x
2)
+ 6(a
px
p+1 + a
p - 1x
p + .... + a
2x
3 + a
1x
2 + a
0x)
+ 8(a
px
p + a
p - 1x
p - 1 + .... + a
2x
2 + a
1x + a
0)
= a
px
p+2 + (a
p - 1+6a
p)x
p + 1 + ........ + (6a
0 + 8a
1)x + 8a
0
Therefore:
P(x) = a
px
p+2 + (a
p - 1+6a
p)x
p + 1 + ........ + (6a
0 + 8a
1)x + 8a
0 + 2x - 11
= a
px
p+2 + (a
p - 1+6a
p)x
p + 1 + ........ + (6a
0 + 8a
1 + 2)x + 8a
0 - 11
=> The degree of P(x) is p + 2
and
F(x) = a
px
p+2 + (a
p - 1+6a
p)x
p + 1 + ........ + (6a
0 + 8a
1)x + 8a
0 + x + 4
= a
px
p+2 + (a
p - 1+6a
p)x
p + 1 + ........ + (6a
0 + 8a
1 + 1)x + 8a
0 + 4
=> The degree of F(x) is p + 2
Therefore the degrees of P(x) and F(x) are equal.
This is probably as rigorous as I can get with this without restating the the very thing that is being proved...
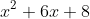 the remainder is 2x-11
the remainder is 2x-11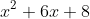 the remainder is x+4
the remainder is x+4