Some Trig Questions (1 Viewer)

nrlwinner · Sep 12, 2009

If you guys could help me solve these, I'd greatly appreciate it.

1. Simplify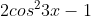 $2cos^23x-1$ (answer is cos6x)

2. Prove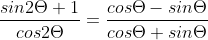 $\frac{sin2\Theta +1}{cos2\Theta }=\frac{cos\Theta -sin\Theta }{cos\Theta +sin\Theta }$

3. Prove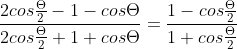 $\frac{2cos\frac{\Theta }{2}-1-cos\Theta }{2cos\frac{\Theta }{2}+1+cos\Theta }=\frac{1-cos\frac{\Theta }{2}}{1+cos\frac{\Theta }{2}}$

4. Prove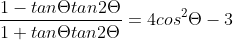 $\frac{1-tan\Theta tan2\Theta }{1+tan\Theta tan2\Theta }=4cos^2\Theta -3$

5. If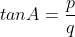 $tanA=\frac{p}{q}$ express in terms of p and q

a)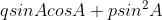 $qsinAcosA+psin^2A$ (answer is p)

b)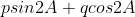 $psin2A+qcos2A$ (answer is q)

6. Find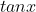 $tanx$ in terms of $tan\Theta$ if $tan\Theta =\frac{cos(\Theta +x)}{cos(\Theta -x)}$

(answer is $\frac{1-tan\Theta }{tan\Theta (1+tan\Theta )}$ )

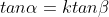7. If $tan\alpha =ktan\beta$ , show that

$(k-1)sin(\alpha +\beta )=(k+1)sin(\alpha -\beta )$

kaz1 · Sep 12, 2009

for 1 use the identity cos2A=2cos²A - 1
for 2 in the RHS multiply top and bottom by cos@-sin@
for 3 in the LHS change the cos@ into cos(@/2)

khorne · Sep 12, 2009

for number2:

2sin@ cos@ + 1/cos^2 @ sin^2 @

2sin@cos@ + cos^2 @ + sin^2 @/cos^2 @ - sin^2@

(sin@ + cos@)(sin@ + cos@)/(cos@ -sin@)(sin@ + cos@)

cancel:
cos + sin / cos - sin

Which is the answer, because this is question 42 in fitzpatrick.

3)
From the t triangle, work out that

cos@/2 = 1/sqrt[1+t^2], or sqrt[1+t^2]/1+t^2
cos@ = 1-t^2/1+t^2

Thus, that becomes

2sqrt[1+t^2] - 1 -t^2 - 1 +t^2/2sqrt[1+t^2] + 1+t^2 + 1 -t^2
simplify and cancel

you get sqrt[1+t^2] - 1/ sqrt[1+t^2] + 1

Now work on other side

1+t^2 - sqrt[1+t^2]/1+t^2 + sqrt[1+t^2]

cancel

gives sqrt[1+t^2] -1/sqrtp1+t^2] + 1

= LHS

Number 4:

This one is pretty tricky:

transform 1 into 1-tan^2/1-tan^2 and tan2@ into 2tan^2/1-tan^2

do that for both numerator/denominator, then cancel all the 1-tan^2

to be left with 1-3tan^2/1+tan^2

Now multiply through by cos^2, to get cos^2-3sin^2/cos^2 + sin^2

thus, cos^2 -3(1-cos^2)

4cos^2 - 3

=LHS

-Note: I stopped writing thetas about half way in...=/

Drongoski · Sep 12, 2009

Q4:

$\100dpi LHS\ \ =\ \ \frac{1\ -\ tan\theta \ tan2\theta }{1\ +\ tan\theta \ tan2\theta }\ \ =\ \ \frac{1-tan\theta\ tan(\theta +\theta )}{1+tan\theta \ tan(\theta +\theta )}\\ \\ =\ \ \frac{1-tan\theta \ \frac{2tan\theta }{1-tan^{2}\theta }}{1+tan\theta \ \frac{2tan\theta }{1-tan^{2}\theta }}\ \ =\ \ \frac{1-tan^{2}\theta \ -\ 2tan^{2}\theta }{1-tan^{2}\theta \ +\ 2tan^{2}\theta }\\ \\ =\ \ \frac{1-3tan^{2}\theta }{1+tan^{2}\theta }\ \ =\ \ \frac{1-3tan^{2}\theta }{sec^{2}\theta }\ \ =\ \ cos^{2}\theta -3sin^{2}\theta \\ \\ =\ \ cos^{2}\theta \ -\ 3(1-cos^{2}\theta )\ \ =\ \ 4cos^{2} \theta -3$

khorne · Sep 12, 2009

My god, what a huge oversight on Question 4...Could have made it so much simpler =/

Question 5:

If tanA = p/q, then y = p, x = q, r = sqrt[p^2+q^2]

thus:

qsinAcosA + psin^2A = q[pq/p^2 + q^2] + p^3/p^2 + q^2

thus, pq^2 + p^3/p^2 + q^2 = p(q^2 + p^2)/p^2 + q^2
= p
Do the other one yourself...it's easy

Question 6:

tan@ = cos@cosx - sin@sinx/cos@cosx + sin@sinx divide by cos@cosx to get 1-tan@tanx/1+tan@tanx

multiply both sides by denominator:

tan@ + tan^2@tanx = 1-tan@tanx

move, and factorise

tan@ [1+tan@tanx + tanx] = 1

1/tan@ = 1+ tanx[tan@ + 1]

1-tan@/tan@ = tanx[tan@ +1]

1-tan@/tan@[tan@ +1] = tanx

xMaFF · Sep 12, 2009

O_________O

Looking at threads like these make me think twice about doing 3 Unit Math next year... *gulp*

You guys are really something.

Drongoski · Sep 12, 2009

Q5

Sorry . . didn't notice Khorne has done this)

$\100dpi using\ right-angled\ \ \Delta: opp = p\ \ \ adj=q \ \ \ hyp= \sqrt{p^{2}+q^{2}}\ \ =\ \ \sqrt{*} \\ \\ \therefore \ \ sinA=\frac{p}{\sqrt{*}}\ \ cosA=\frac{q}{\sqrt{*}}\\ \\ a)\ \ qsinAcosA+psin^{2}A\ \ =\ \ q\cdot \frac{p}{\sqrt{*}}\cdot \frac{q}{\sqrt{*}}\ +\ p\cdot \frac{p^{2}}{(\sqrt{*})^{2}}\\ \\ =\ \ \frac{pq^{2}}{p^{2}+q^{2}}\ +\ \frac{p^{3}}{p^{2}+q^{2}}\ =\ \frac{p(p^{2}+q^{2})}{p^{2}+q^{2}}\ \ =\ \ p\\ \\ \\ b)\ \ psin2A\ +\ qcos2A\ \ =\ \ p(2sinAcosA)\ +\ q(1-2sin^{2}A)\\ \\ =\ \ 2p\cdot \frac{p}{\sqrt{*}}\cdot \frac{q}{\sqrt{*}}\ +\ q(1-\frac{2p^{2}}{*})\ \ =\ \ \frac{2p^{2}q+qp^{2}+q^{3}-2p^{2}q}{p^{2}+q^{2}}\ =\ q$

khorne · Sep 12, 2009

xMaFF said:
O_________O

Looking at threads like these make me think twice about doing 3 Unit Math next year... *gulp*

You guys are really something.

Not as hard as it looks.

Drongoski · Sep 12, 2009

khorne said:
Not as hard as it looks.

Indeed. Proving trig identities of this type is really easy.

Trebla · Sep 12, 2009

For Q7:

$\tan \alpha = k\tan \beta\\\\\Rightarrow \dfrac{\sin \alpha}{\cos \alpha}= k\dfrac{\sin \beta}{\cos \beta}\\\\\sin \alpha \cos \beta = k \sin \beta \cos \alpha\\\\LHS = (k-1)\sin (\alpha+\beta)\\\\= (k - 1)(\sin \alpha \cos \beta + \sin \beta \cos \alpha)\\\\= k\sin \alpha \cos \beta + k\sin \beta \cos \alpha - \sin \alpha \cos \beta - \sin \beta \cos \alpha\\\\=k\sin \alpha \cos \beta + k\sin \beta \cos \alpha - k \sin \beta \cos \alpha - \sin \beta \cos \alpha\\\\= k\sin \alpha \cos \beta - k\sin \beta \cos \alpha + k\sin \beta \cos \alpha - \sin \beta \cos \alpha\\\\= k(\sin \alpha \cos \beta - \sin \beta \cos \alpha) + k\sin \beta \cos \alpha - \sin \beta \cos \alpha\\\\= k\sin (\alpha-\beta)+ \sin \alpha \cos \beta - \sin \beta \cos \alpha\\\\= k\sin (\alpha-\beta) + \sin (\alpha-\beta)\\\\= (k+1)\sin (\alpha-\beta)\\\\= RHS$

nrlwinner · Sep 12, 2009

thanks guys. can someone explain question 3 for me cauz i still dont get it.

Drongoski · Sep 12, 2009

nrlwinner said:
thanks guys. can someone explain question 3 for me cauz i still dont get it.

OK. I'll do it now.

Drongoski · Sep 12, 2009

To understand you need remember the double-angle identities below:
[1st one not here required]

$\100dpi 1 - cos\theta\ \equiv 1-cos(2\times \frac{\theta }{2})\ \equiv \ 2sin^{2}\frac{\theta }{2}\\ \\ Similarly:\ \ 1+cos\theta \ \equiv\ 2cos^{2}\frac{\theta }{2}\\ \\ \therefore \ \ LHS\ =\ \frac{2cos\frac{\theta }{2}-2cos^{2}\ \frac{\theta }{2}}{2cos\frac{\theta }{2}+2cos^{2}\ \frac{\theta }{2}}\ \ =\ \ \frac{2cos\frac{\theta }{2}(1-cos\frac{\theta }{2})}{2cos\frac{\theta }{2}(1+cos\frac{\theta }{2})}\ =\ \frac{1-cos\frac{\theta }{2}}{1+cos\frac{\theta }{2}}\ =\ RHS$

ps: khorne's solution uses the half-angle t-formulae (a version of the double angle formulae) which you
may not have learnt yet.That may be why you were unable to follow his solution.

Make a Difference – Donate to Bored of Studies!

Some Trig Questions (1 Viewer)

nrlwinner

Member

kaz1

et tu

khorne

Guest

Drongoski

Well-Known Member

khorne

Guest

xMaFF

Member

Drongoski

Well-Known Member

khorne

Guest

Drongoski

Well-Known Member

Trebla

Administrator

nrlwinner

Member

Drongoski

Well-Known Member

Drongoski

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 1)