jessica2011hsc
Member
- Joined
- Feb 13, 2011
- Messages
- 42
- Gender
- Female
- HSC
- 2011
my school is behind in this topic, so im trying to accelerate. that's why i asked this question, cause im not completely sure how to do it with confidence
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
my school is behind in this topic, so im trying to accelerate. that's why i asked this question, cause im not completely sure how to do it with confidence
lol: know yu cant said 2, unit mths is piss esyP(x)=ax^3+bx^2+cx+d P(0) = 5 = d
P'(x)=3ax^2+2bx+c
0 = 3ax^2 + 2bx + c for stat points.
0 = 3a + 2b + c 0 = 12a - 4b + c
12a - 3a - 4b -2 b + c - c = 0
9a - 6b = 0
3a - 2b = 0
P(1) = 12 P(-2) = 15
Hence, a + b + c + d = 12 -8a + 4b - 2c + d = 15
a + 8a + b - 4b + c + 2c + d - d = 12 - 15
9a - 3b + 3c = -3
3a - b + c = -1
3a - 3a + b + 2b + c - c = 0 + 1
3b = 1
b = 1/3
9a - 5(1/3) = 0
9a = 2.5
a = 5/27
3(5/27) - 1/3 + c = -1
c = -1 - 15/27 + 1/3
c = -11/9
a + b + c + d = 12
5/27 + 1/3 - 11/9 + d = 12
d = 12 - 5/27 -1/3 + 11/9
This is wrong... lol
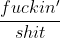
I haven't worked it out, but from the line:
Stationary when
Substitute back,

this i'm am finding difficulty. please provide some form of help : [Make y the subject,find intersection points and graph it. Then you just do it
What is wrong with your language?lol: know yu cant said 2, unit mths is piss esy
Lmao
x^2 +4x + 4 = 4x - x^2(x+2)^2 = 4x-x^2
Then solve
lol thats the worst display of algebra I have ever seen(x+2)(x+2) = x^2 + 4x + 4
therefore x = 4x - x^2 - 2
To all above attempting this question, learn to read properly.Question: http://imgur.com/SZkDD
um hii guys, I'm stuck on this question and don't know what the intercept of the 2 curves are. thankss
Ha, no it was just me. I think they assumed what I was saying was correctTo all above attempting this question, learn to read properly.
differentiate <a href="http://www.codecogs.com/eqnedit.php?latex=\displaystyle x\sqrt{x@plus;1}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\displaystyle x\sqrt{x+1}" title="\displaystyle x\sqrt{x+1}" /></a>
