Circle Geometry questions (1 Viewer)

[artosis]

help please... my trials in 2 days

 

[woga1]

they are too easy.

 

[artosis]

they are too easy.

can u post up the solution? plz

 

[woga1]

sorry im a cunt!

 

[HyperComplexxx]

1/
i. BAC = YAX =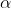 (V.opp angles)
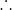BAC = BPC = 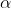(angle on same arc)
ii. BPC = OPN =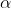 (v.opp angles)
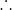OPN = OMN = 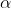(angle on same arc)
iii. YAX = XMY =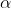 - angle on same segment are equal
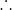XYAM is cyclic quad.
iv. XAM = BCP (ext. angle of cyclic quad ABCP = opp. interior angle)
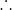angle XYM = XAM = BCP (angle on same arc)
v. let angle XMA =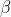
XYA = 180 - 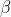(opp. angles of cyclic quad XYAM are supp.)
Consider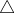 CZO
ZOC = XMP =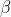 (ext. angle of cyclic quad ONMP = opp. int. angle)
But ZCO = XYM (from iv)
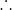CZO = 180 - 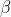- XYM = CYO
hence COYZ is a cyclic quid. angle on same segment are equal
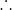ZYC = ZOC = (angle on same segment are equal) =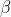
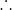ZYX = ZYC + XYA 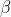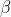= + 180 - = 180
Thefore Z,Y,Z are collinear

Second question part iv = mindblown

 

[artosis]

Thanks!

Im still trying to comprehend part (v)
my minds going in circles trying to figure out what you're doing lol. (no pun intended)

any hope on question 2?

 

[Hermes1]

Do u still want question 2 done i no how to do it i just need confirmation

 

[artosis]

my teacher got it from some trial paper, im guessing
these questions are from the revision sheet she gave me

 

[Hermes1]

This is my proof for part i of 2.
OV = OW (equal radii)
PV = PW (tangents drawn from an external point equal)
OP is common
therefore triangle OPW congruent to triangle OPV (SSS)
therefore angle WOM = angle MOV (corresponding angles congruent triangles equal)
OV = OW
OM is common
therefore triangle MOV congruent to triangle MOW (SAS)

therefore MW = MV (corresponding sides congruent triangles equal)
therefore OM perpendicular to VW (line through centre which bisects a chord is perpendicular to it)

 

[largarithmic]

The first question is a direct consequence of http://en.wikipedia.org/wiki/Desargues'_theorem

The second question is a well known result, http://en.wikipedia.org/wiki/Radical_axis. To do part (iv):

Let AB and CD intersect at X; it remains to prove X lies on EF.

From part (iii), the following are true:
(1) XO^2 - XP^2 = r^2 - s^2, as X lies on AB;
(2) XP^2 - XQ^2 = s^2 - t^2, as X lies on CD.

Adding (1) and (2), we obtain XO^2 - XQ^2 = r^2 - t^2, which then from (iii) implies X lies on EF.
It directly follows then that AB, CD, EF are concurrent.

 

[artosis]

This is my proof for part i of 2.
OV = OW (equal radii)
PV = PW (tangents drawn from an external point equal)
OP is common
therefore triangle OPW congruent to triangle OPV (SSS)
therefore angle WOM = angle MOV (corresponding angles congruent triangles equal)
OV = OW
OM is common
therefore triangle MOV congruent to triangle MOW (SAS)

therefore MW = MV (corresponding sides congruent triangles equal)
therefore OM perpendicular to VW (line through centre which bisects a chord is perpendicular to it)

ty!!!!
(I tried to rep u, but its not letting me)


dw about the rest of them. part ii onwards seem stupid.

 

[Hermes1]

ty!!!!
(I tried to rep u, but its not letting me)


dw about the rest of them. part ii onwards seem stupid.

yeh lol, u cant rep ppl till you get rep power urself.

 

[Omnipotence]

Repped him for you.

 

[largarithmic]

part ii onwards seem stupid.

In what sense?

 

[artosis]

Repped him for you.

ty

In what sense?

those theorems u linked to arent part of the hsc syllabus...

 

[largarithmic]

those theorems u linked to arent part of the hsc syllabus...

The vast majority of HSC geometry problems are either special cases or direct proofs of theorems not in the syllabus; compare last year's q7 from the 4u paper with http://en.wikipedia.org/wiki/Ptolemy's_theorem. Clearly the question is no more or less stupid as a result.