-
Looking for HSC notes and resources? Check out our Notes & Resources page
Locus and the Parabola! (1 Viewer)
- Thread starter jnney
- Start date
Hermes1
Banned
- Joined
- Oct 4, 2010
- Messages
- 1,282
- Gender
- Male
- HSC
- 2011
you ll have two parabolas, once concave up and one concave downGood evening,
The latus rectum of a parabola has endpoints (-2, 3) and (6,3). Find two possible equations for the parabola.
I found the focus to be (2,3). That's all.
Hermes1
Banned
- Joined
- Oct 4, 2010
- Messages
- 1,282
- Gender
- Male
- HSC
- 2011
okay so one will be:yes I know.
(x-2)^2 = 8(y-1)
another:
(x-2)^2 = -8(y-5)
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
The distance will be 8 from point to point.
So,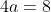 (Remembering the latus rectum is 4 times the focal length.)
(Remembering the latus rectum is 4 times the focal length.)
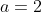 . Our focal length.
. Our focal length.
We can see that the focus is at the midpoint of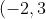) and
and 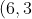) .
.
The midpoint is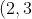) . [Note: This is our focus.]
. [Note: This is our focus.]
We know that our focal length is 2.
We also know that the latus rectum is parallel to the x axis,
So it will have the form,
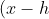^2= \pm 4a(y-k))
Let us consider the positive case first,
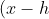^2=4a(y-k))
So we know that the focus is 2 units from the vertex. If it is concave up, it will be two units down.
Hence, vertex is at.)
Our equation will be,
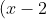^2=8(y-1))
Consider the negative case,
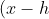^2=-4a(y-k))
Since it is concave down, we would expect the vertex to be above the focus by 2 units.
Hence the vertex is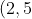) .
.
Therefore our equation is,
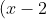^2=-8(y-5))
So,
We can see that the focus is at the midpoint of
The midpoint is
We know that our focal length is 2.
We also know that the latus rectum is parallel to the x axis,
So it will have the form,
Let us consider the positive case first,
So we know that the focus is 2 units from the vertex. If it is concave up, it will be two units down.
Hence, vertex is at
Our equation will be,
Consider the negative case,
Since it is concave down, we would expect the vertex to be above the focus by 2 units.
Hence the vertex is
Therefore our equation is,
Last edited:
Hermes1
Banned
- Joined
- Oct 4, 2010
- Messages
- 1,282
- Gender
- Male
- HSC
- 2011
you know how you have the parabola in the form x^2 = 4ayHow did you find 'a' and the y intercept?
well the 4a is the length of the latus rectum.
here you can see that the latus rectum is the length of the interval from (6, 3) to (-2,3)
hence the latus rectum is 8 units.
also you know that a = focal length (distance between vertex and focus).
4a = 8
a = 2
focus (2,3) therefore one vertex is at (2,1) and another at (2, 5)
and these parabolas are in the form (x-h)^2 = 4a(y-k) where 4a is the latus rectum and (h, k) is the vertex
therefore you have (x-2)^2 = 8(y-1)
(x-2)^2 = -8(y-5)
Hermes1
Banned
- Joined
- Oct 4, 2010
- Messages
- 1,282
- Gender
- Male
- HSC
- 2011
this. man latex looks so much better.The distance will be 8 from point to point.
So,(Remembering the latus rectum is 4 times the focal length.)
. Our focal length.
We can see that the focus is at the midpoint ofand
.
The midpoint is. [Note: This is our focus.]
We know that our focal length is 2.
We also know that the latus rectum is parallel to the x axis,
So it will have the form,
Let us consider the positive case first,
So we know that the focus is 2 units from the vertex. If it is concave up, it will be two units down.
Hence, vertex is at
Our equation will be,
Consider the negative case,
Since it is concave down, we would expect the vertex to be above the focus by 2 units.
Hence the vertex is.
Therefore our equation is,
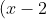^2=-8(y-5))
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
It also takes much longer. I might stop helping now.
Hermes1
Banned
- Joined
- Oct 4, 2010
- Messages
- 1,282
- Gender
- Male
- HSC
- 2011
what do u mean. stop helping ppl for gud?It also takes much longer. I might stop helping now.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
From now on.what do u mean. stop helping ppl for gud?
