starryblue
Member
can anyone please tell me how to graph the curve y=log10(x+1)?
thank you~
thank you~
Students helping students, join us in improving Bored of Studies by donating and supporting future students!

Google images.What program is that spi?
oh! i get it! *sigh* i got saved by you again!First of all you have to see what a general logarithmic curve looks like. It will look something like this.

You will see that the graph is this shape if you graph some points.
The asymptote is atand it must go past through the point
. So why is the asymptote zero?
If we look at our graphand rewrite it as indice form,
Ifwas zero, then,
This value ofdoes not exist. Since you always get a number above zero.
Let's think back to parabolas.
Say we have the curve. Our original graph was
We can see that the addition of 1 moves it to the left ONE unit.
Back to our curve. Applying this, we can see it will move one space to the left.
Normally that logarithmic curve will have an asmyptote atand must go through
. In this case, the asymptote moves one place, hence it is now at
and the
intercept is now at
Your graph should look something like this.
http://imageshack.us/photo/my-images/193/forstarryblue.png/
Note: Why did I plot one point? This is to avoid confusion since graphs of logarithms with different bases look similar.
Example - Unless you have a good eye, when graphing separatelyor
, it is quite difficult to tell which graph is which, but if a point was plotted, this gives the marker a general idea.
More general, if we have the curveoh! i get it! *sigh* i got saved by you again!
ahh == mayb i should of mentioned earlier but i knew that, it's just that i didn't know what to plot but you answered that...how about for hyperbolas? if it was eg. y=2/x, then what would u plot?More general, if we have the curve
moves to the left
units if
moves to the right
units if
moves it up
units if
moves it down
units if
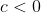
Does your coaching college expect you to use the formal way to graph this? In year 10 you only do a generalised way. I will teach you the formal way in a second. When my hand does not feel sore.ahh == mayb i should of mentioned earlier but i knew that, it's just that i didn't know what to plot but you answered that...how about for hyperbolas? if it was eg. y=2/x, then what would u plot?
O.O" there's a formal way? is that more difficult to do? btw, how do you find the range of a graph?Does your coaching college expect you to use the formal way to graph this? In year 10 you only do a generalised way. I will teach you the formal way in a second. When my hand does not feel sore.
oh ok, no wonder it doesn't make sense...do you need to dot x=0 since its the asymptote?
First step is always find theand
intercepts, if there are any.
and
intercepts: When you let[
to find the
intercept and
to find the
intercept, you can see that the value does not exist.
The next step is to find any asymptotes. It is convenient for me to find the vertical asymptote first.
Vertical asymptote:
Now,
A vertical asymptote occurs when the denominator equals to zero.
[That is our asymptote.]
Your graph should look like this:
Now next stage is to find how the graph behaves near the vertical asymptote.
Behaviour: To do this we must see the tendency of the curve as it approaches the asymptote to the left and to the right.
We will test the behaviour near its immediate left first. So what is a number close to the left of zero? I know -0.1.
[A positive number divide a positive number is a positive number.]
You get a positive number.
So,
As[As
gets close to zero from the left hand side.]
[
tends to positive infinity.]
EDITING: Don't read until I am done and finished editing my mistakes.
Don't read just yet, I need to make a few adjustments.oh ok, no wonder it doesn't make sense...do you need to dot x=0 since its the asymptote?
oks =) take your time~Don't read just yet, I need to make a few adjustments.
Should be okay to read now, I will see if I made any silly errors.oks =) take your time~
you rote: We will test the behaviour near its immediate left first. So what is a number close to the left of zero? I know -0.1.Should be okay to read now, I will see if I made any silly errors.
Where did I write that? Quote and bold it.you rote: We will test the behaviour near its immediate left first. So what is a number close to the left of zero? I know -0.1.
[A positive number divide a positive number is a positive number.]
You get a positive number.
umm....wouldn't it be a positive number divided by a negative number since you said the left of 0, ie. -0.1?
==" i swear it was something else before~ nvm i got it! tys~
First step is always find theand
intercepts, if there are any.
and
intercepts: When you let
to find the
intercept and
to find the
intercept, you can see that the value does not exist.
The next step is to find any asymptotes. It is convenient for me to find the vertical asymptote first.
VERTICAL ASYMPTOTE
Now,
A vertical asymptote occurs when the denominator equals to zero.
[That is our asymptote.]
Your graph should look like this:
http://www.mediafire.com/?faa36hb8slbncv2
Now next stage is to find how the graph behaves near the vertical asymptote.
Behaviour: To do this we must see the tendency of the curve as it approaches the asymptote to the left and to the right.
BEHAVIOUR
We will test the behaviour near its immediate left first. So what is a number close to the left of zero? I know -0.1.
[A positive number divide a negative number is a negative number.]
You get a negative number.
So,
As[As
gets close to zero from the left hand side.]
[
tends to negative infinity.]
We will now test the behaviour to the immediate right. So what is a number close to the right of zero? I know 0.1.
[A positive number divide a positive number is a positive number.]
You get a positive number.
So,
As[As
gets close to zero from the right hand side.]
[
tends to positive infinity.]
Your graph should look something like this:
http://www.mediafire.com/?0o2nrnamc3qc3xe
Now horizontal asymptote.
HORIZONTAL ASYMPTOTE AND TENDENCY
We must find what happens when the graph tends to positive infinity. To help you understand this, substitute a large positive number into the equation of graph. Let's use 1000.
[Something like that, we can see it's a small figure close to zero above.]
So,
As. [As
approaches positive infinity.]
[
approaches zero a bit above it.]
We must find what happens when the graph tends to negative infinity. To help you understand this, substitute a large negative number into the equation of graph. Let's use -1000.
[Something like that, we can see it's a small figure close to zero below it.]
So,
As. [As
approaches negative infinity.]
[
approaches zero a bit below it.]
Now your graph should look like:
http://www.mediafire.com/?h5c4kcmekh3dgcl
Now all you have to do is connect the points. Make sure you indicate a point. Use something like
http://www.mediafire.com/?d8uuceefrz5t3nc
Are you sure? Feel free to ask any more questions. I said I was in the process of editing it.==" i swear it was something else before~ nvm i got it! tys~
