Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
complex (1 Viewer)
- Thread starter jnney
- Start date
Fus Ro Dah
Member
- Joined
- Dec 16, 2011
- Messages
- 247
- Gender
- Male
- HSC
- 2013
If you expand the cis into cosx + isinx, then z = 2i, and w = -1 + sqrt(3).i
z - w = 2i - (-1 + sqrt(3).i )
= 1 + i ( 2 - sqrt(3) )
Arg (z-w) = Arg (1 + i ( 2 - sqrt(3) ) ) = arctan (2 - sqrt(3) )
Note: arctan is a short hand way of saying inverse tan.
Edit: Which is equal to pi/12, I forgot to mention that. It's something that you just remember after doing a shitload of trig questions.
z - w = 2i - (-1 + sqrt(3).i )
= 1 + i ( 2 - sqrt(3) )
Arg (z-w) = Arg (1 + i ( 2 - sqrt(3) ) ) = arctan (2 - sqrt(3) )
Note: arctan is a short hand way of saying inverse tan.
Edit: Which is equal to pi/12, I forgot to mention that. It's something that you just remember after doing a shitload of trig questions.
Last edited:
Fus Ro Dah
Member
- Joined
- Dec 16, 2011
- Messages
- 247
- Gender
- Male
- HSC
- 2013
Alternatively, you can construct the vector z-w (using vector addition and subtraction), and then use basic Euclidean Geometry to prove that Arg(z-w) is 15 degrees (or pi/12)
1. Draw the usual parallelogram, including z-w.
2. Notice that Arg(w) = 2pi/3, which means that the bigger angle of the parallelogram is simply 2pi/3 + pi/2 = 7pi/6
3. We divide this by 2 because the vector z-w bisects this big angle, giving us 7pi/12
4. Arg (z-w) is the 'excess' of this after taking away 90 degrees (pi/2), leaving us Arg (z-w) = pi/12
Sorry if this is a bit ambiguous. I have included a diagram which may or may not help.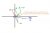
1. Draw the usual parallelogram, including z-w.
2. Notice that Arg(w) = 2pi/3, which means that the bigger angle of the parallelogram is simply 2pi/3 + pi/2 = 7pi/6
3. We divide this by 2 because the vector z-w bisects this big angle, giving us 7pi/12
4. Arg (z-w) is the 'excess' of this after taking away 90 degrees (pi/2), leaving us Arg (z-w) = pi/12
Sorry if this is a bit ambiguous. I have included a diagram which may or may not help.

pokka
d'ohnuts
- Joined
- Nov 4, 2011
- Messages
- 311
- Gender
- Female
- HSC
- 2011
If you expand the cis into cosx + isinx, then z = 2i, and w = -1 + sqrt(3).i
z - w = 2i - (-1 + sqrt(3).i )
= 1 + i ( 2 - sqrt(3) )
Arg (z-w) = Arg (1 + i ( 2 - sqrt(3) ) ) = arctan (2 - sqrt(3) )
Note: arctan is a short hand way of saying inverse tan.
Edit: Which is equal to pi/12, I forgot to mention that. It's something that you just remember after doing a shitload of trig questions.
Last edited:
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
However, your method does not yield an exact solution, which is far more preferable over an approximation.
Fus Ro Dah's (lol @ name) second method is right, and it gives you the exact value, but he explained it kinda crap. Can't blame him though, geometry proofs via typing have never been too easy to do when compared to algebraic proofs.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
I'm quite convinced that it's a guy, looking at the name and DP.Fus Ro Dah's (lol @ name) second method is right, and it gives you the exact value, but he explained it kinda crap.
pokka
d'ohnuts
- Joined
- Nov 4, 2011
- Messages
- 311
- Gender
- Female
- HSC
- 2011
I think this is best way to do this question (Y)

