-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Quick question on inverse functions (1 Viewer)
- Thread starter Jackson94
- Start date
RealiseNothing
what is that?It is Cowpea
y = -x^3
It's inverse is when you swap the x and y around so:
x = -y^3
Make y the subject:
y = cube root of -x
Now solving simultaneously:
-x^3 = cube root of -x
-x^9 = -x (Cube both sides)
x^9 = x
x = -1, 0, or 1
It's inverse is when you swap the x and y around so:
x = -y^3
Make y the subject:
y = cube root of -x
Now solving simultaneously:
-x^3 = cube root of -x
-x^9 = -x (Cube both sides)
x^9 = x
x = -1, 0, or 1
Last edited:
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
Lol why are you waiting for me?y = -x^3
It's inverse is when you swap the x and y around so:
x = -y^3
Make y the subject:
y = cube root of -x
Now solving simultaneously:
-x^3 = cube root of -x
-x^9 = -x (Cube both sides)
x^9 = x
x = -1, 0, or 1
Will wait for Spiral or some one to confirm since I'm not 100% sure this is right.
deterministic
Member
- Joined
- Jul 23, 2010
- Messages
- 423
- Gender
- Male
- HSC
- 2009
EDIT: nevermind see above
Last edited:
RealiseNothing
what is that?It is Cowpea
Because I know you'll come in here and teach him everything from scratch lolLol why are you waiting for me?
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
I interpret the question that is punctuated incorrectly as
Find where the function and its inverse intersect.
Find where the function and its inverse intersect.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
I would also state in Cartesian coordinate form.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
The inverse function is drawn by flipping the curve about the line y=x or y=-x.
This means that when it intersects its inverse, it also intersects the line y=x or y=-x.
So all you have to do is solve the pair of simultaneous equations y=-x^3 and y=x or y=-x (depends on the Q) in order to find the inverse intercept.
I have provided a bit of a diagram to help you see it: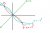
Instead of solving simultaneously the equation of the curve and its inverse, you can simply do it with the equation of the curve, and the line y=x or y=-x, since that's where it intersects the inverse anyway.
Here is another example for you to see:
EDIT: Yes, you will have to restrict the domain yourself. You will acquire two solutions, but you cannot have both. Which branch you choose however, will depend on the question.
This means that when it intersects its inverse, it also intersects the line y=x or y=-x.
So all you have to do is solve the pair of simultaneous equations y=-x^3 and y=x or y=-x (depends on the Q) in order to find the inverse intercept.
I have provided a bit of a diagram to help you see it:

Instead of solving simultaneously the equation of the curve and its inverse, you can simply do it with the equation of the curve, and the line y=x or y=-x, since that's where it intersects the inverse anyway.
Here is another example for you to see:

EDIT: Yes, you will have to restrict the domain yourself. You will acquire two solutions, but you cannot have both. Which branch you choose however, will depend on the question.
Attachments
-
60 KB Views: 58
Last edited:
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,960
- Gender
- Female
- HSC
- N/A
The second example is not an inverse function unless you restrict it.The inverse function is drawn by flipping the line about the line y=x.
This means that when it intersects its inverse, it also intersects the line y=x.
So all you have to do is solve the pair of simultaneous equations y=-x^3 and y=x in order to find the inverse intercept.
I have provided a bit of a diagram to help you see it: View attachment 24028
Instead of solving simultaneously the equation of the curve and its inverse, you can simply do it with the equation of the curve, and the line y=x, since that's where it intersects the inverse anyway.
Here is another example for you to see: View attachment 24029
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Yes I know it is not a function by definition due to the unrestricted domain, but it's so he can properly see the action of the 'flipping', and how it yields two solutions. If you restrict the domain beforehand, then you may miss out on solutions.The second example is not an inverse function unless you restrict it.
In exams, I draw the whole thing unrestricted (on the edge of the page just for myself to see), THEN I restrict the domain according to the question (if it specifies which branch. If it doesn't, then I write down the 2 possible cases)
Last edited:
largarithmic
Member
- Joined
- Aug 9, 2011
- Messages
- 202
- Gender
- Male
- HSC
- 2011
I think "find the intersection of a curve and its inverse" and "find the intersection of a function and its inverse function" are two pretty different questions... in particular the former is much nastier. try find the intersection of y = 10x^3 - 10x for instance and its inverse x = 10y^3 - y. You'll give yourself a serious headache (there are nine solutions!)
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
lol but this is the HSC. Asif they will expect that of a student.I think "find the intersection of a curve and its inverse" and "find the intersection of a function and its inverse function" are two pretty different questions... in particular the former is much nastier. try find the intersection of y = 10x^3 - 10x for instance and its inverse x = 10y^3 - y. You'll give yourself a serious headache (there are nine solutions!)
If you put the two curves you mentioned (with unrestricted domain) on a graphing program, you will see a 2x2 grid sorta thing. It would be a very interesting question to try to find the area of that '2x2' grid.
largarithmic
Member
- Joined
- Aug 9, 2011
- Messages
- 202
- Gender
- Male
- HSC
- 2011
oooh thats legit... Id imagine you could cut it up and integrate it?lol but this is the HSC. Asif they will expect that of a student.
If you put the two curves you mentioned (with unrestricted domain) on a graphing program, you will see a 2x2 grid sorta thing. It would be a very interesting question to try to find the area of that '2x2' grid.
alsoooooo this reminds me, you know theres an awesome theorem about the intersection of two cubics? http://en.wikipedia.org/wiki/Cayley–Bacharach_theorem
lots of random geometric results are made almost trivial by that awesome theorem - you can treat things like a triple of lines, for instance, as a single cubic eqn e.g. (x+y-1)(x+2y-3)(x-4y+5) = 0 is a set of 3 lines, or a circle and a line e.g. (x^2+y^2-1)(x+y-1)=0. For example http://en.wikipedia.org/wiki/Pivot_theorem is a special case
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
I've run across that theorem before when I randomly browse Maths articles on Wikipedia (I know it sounds sad, but it is actually quite interesting!). It would be interesting to have an elementary proof of it appear in the HSC.oooh thats legit... Id imagine you could cut it up and integrate it?
alsoooooo this reminds me, you know theres an awesome theorem about the intersection of two cubics? http://en.wikipedia.org/wiki/Cayley–Bacharach_theorem
lots of random geometric results are made almost trivial by that awesome theorem - you can treat things like a triple of lines, for instance, as a single cubic eqn e.g. (x+y-1)(x+2y-3)(x-4y+5) = 0 is a set of 3 lines, or a circle and a line e.g. (x^2+y^2-1)(x+y-1)=0. For example http://en.wikipedia.org/wiki/Pivot_theorem is a special case
Also regarding the area problem, there must be an easier way. The cutting up and integrating is too... brute force. Not elegant.
largarithmic
Member
- Joined
- Aug 9, 2011
- Messages
- 202
- Gender
- Male
- HSC
- 2011
reading maths articles on wikipedia is never a bad thing! I heard the guy who wrote the q8 this year based it on a theorem he found on wikipediaI've run across that theorem before when I randomly browse Maths articles on Wikipedia (I know it sounds sad, but it is actually quite interesting!). It would be interesting to have an elementary proof of it appear in the HSC.