Functions (1 Viewer)

[Coookies]

Consider the function f(x). If f(0) = 0, f '(x)>0 and f ''(x)<0, make a neat sketch of f(x) near x=0




Im not good at this stuff. Is this just a parabola with vertex (0,0)? It says "near x=0" so Im not sure

 

[Timske]

If f(0) = 0, f '(x)>0 and f ''(x)<0, make a neat sketch of f(x) near x=0.

When f'x > 0 - the curve is increasing and when f ''x < 0 the curve is concave down.

f(0) = 0 means it goes through (0,0)

 

[Coookies]

So parabola right?

 

[Carrotsticks]

Consider the function f(x). If f(0) = 0, f '(x)>0 and f ''(x)<0, make a neat sketch of f(x) near x=0

Math: f(0) = 0

English: When x=0. y=0. So the curve passes through the origin.



Math: f'(x) > 0

English: The curve always has a positive gradient ie: it is an increasing function.




Math: f''(x) < 0

English: The curve is concave down.



A parabola (either positive or negative) does not satisfy all these conditions because no (unrestricted) parabola always has f'(x) > 0.

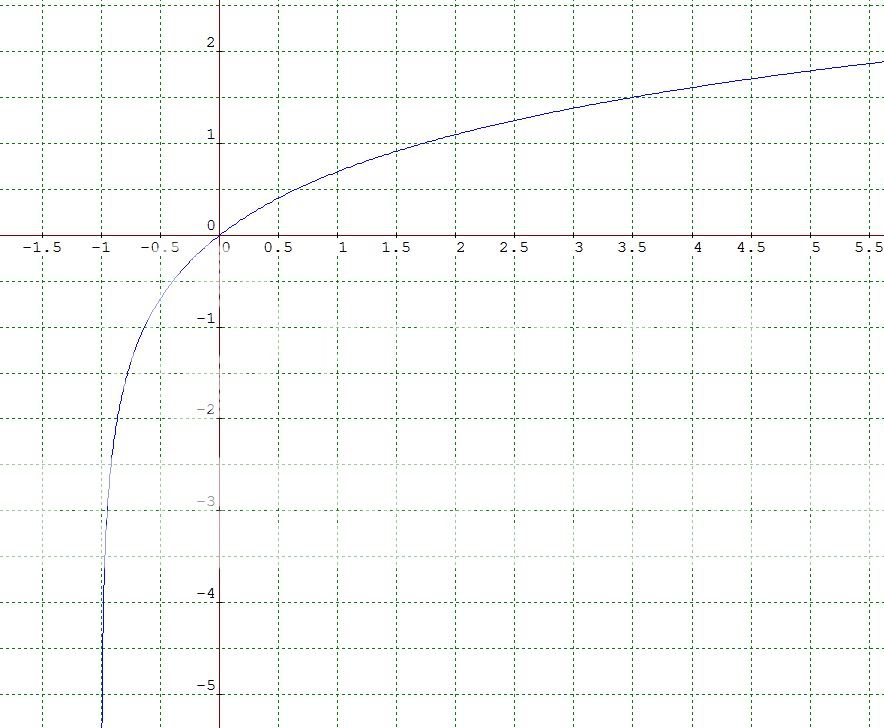
Try the curve y = ln(1+x)

 

[Coookies]

I haven't done y = ln(1+x) yet, what does it look like?

 

[Timske]

^
y = x^2
y'' = 2

2 > 0

 

[Timske]

http://www.wolframalpha.com/input/?i=y+=+ln(x++1)

this satisfy all the conditions.

u can see it goes through the origin, its increasing and its concave down

 

[Carrotsticks]

I haven't done y = ln(1+x) yet, what does it look like?

^
y = x^2
y'' = 2

2 > 0

Parabola can be negative too.

 

[Coookies]

^ THANKS!