See questions below, thanks
1. If a > o, b> 0 and c>0, show that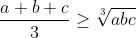
2. Show that, if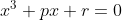 has a root of multiplicity two, then
has a root of multiplicity two, then 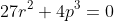
3. Show that^{2})
4. Find the roots of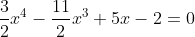
5. In the diagram, the bisector of the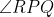 meets RQ in S and the circum-circle of the triangle PQR in T.
meets RQ in S and the circum-circle of the triangle PQR in T.
Prove that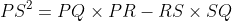
6.
AB is the common chord of two circles C1 and C2. AC and AD are chords of the respective circles with
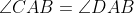 and CD meets the circles at P and Q respectively. R is the foot of the perpendicular from P to BQ. Prove that
and CD meets the circles at P and Q respectively. R is the foot of the perpendicular from P to BQ. Prove that 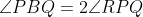
q 5 and 6 diagrams : View attachment 24582View attachment 24581
1. If a > o, b> 0 and c>0, show that
2. Show that, if
3. Show that
4. Find the roots of
5. In the diagram, the bisector of the
Prove that
6.
AB is the common chord of two circles C1 and C2. AC and AD are chords of the respective circles with
q 5 and 6 diagrams : View attachment 24582View attachment 24581
