-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Math Question ! (1 Viewer)
- Thread starter SGSII
- Start date
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Did you mean:

or

or
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
1. Make sure numerator is of lower degree than denominator
2. Odd/Even/Neither?
3. x & y intercepts
4. Vertical asymptotes
a) Test behaviour at vertical asymptotes
5. Behaviour as x -> + or - infinity
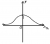
Using these steps, 1. is fulfilled.
2. f(-x) = f(x) so it is even (symmetrical about y-axis)
3. When x = 0, y = 1 so y intercept is (0, 1). When y = 0, 0 = 1 which cannot be possible so there is no y intercept and there is a horizontal asymptote at y = 0
4. Denominator cannot equal to zero as you cannot solve x^2 + 1 = 0
5. As x -> infinity, 1 / (x^2 + 1) -> 0+ (the plus meaning it is slightly above 0)
As x -> -infinity, 1 / (x^2 + 1) -> 0+
So now you're left with this,

From this, we can "join the dots" smoothly in to a nice curve.

2. Odd/Even/Neither?
3. x & y intercepts
4. Vertical asymptotes
a) Test behaviour at vertical asymptotes
5. Behaviour as x -> + or - infinity
Using these steps, 1. is fulfilled.
2. f(-x) = f(x) so it is even (symmetrical about y-axis)
3. When x = 0, y = 1 so y intercept is (0, 1). When y = 0, 0 = 1 which cannot be possible so there is no y intercept and there is a horizontal asymptote at y = 0
4. Denominator cannot equal to zero as you cannot solve x^2 + 1 = 0
5. As x -> infinity, 1 / (x^2 + 1) -> 0+ (the plus meaning it is slightly above 0)
As x -> -infinity, 1 / (x^2 + 1) -> 0+
So now you're left with this,

From this, we can "join the dots" smoothly in to a nice curve.

Attachments
-
7.7 KB Views: 111
RivalryofTroll
Sleep Deprived Entity
- Joined
- Feb 10, 2011
- Messages
- 3,804
- Gender
- Male
- HSC
- 2013
- Uni Grad
- 2019
RealiseNothing
what is that?It is Cowpea
A really weird way that you might be able to use (although probably much harder), is to graph 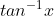 , and then differentiate the graph since:
, and then differentiate the graph since:


Use the graphing a derivative method or whatever it's called.
Use the graphing a derivative method or whatever it's called.
Last edited:
professorayton8
Member
- Joined
- Apr 28, 2012
- Messages
- 111
- Gender
- Female
- HSC
- 2013
Hi!  i have a similar question to the question asked in this thread.how do you know what the graph looks like when you find out all the asymptotes, intercepts etc.?and what does 'symmetrical about the y and origin' mean?- how does it affect the graph?thanks
i have a similar question to the question asked in this thread.how do you know what the graph looks like when you find out all the asymptotes, intercepts etc.?and what does 'symmetrical about the y and origin' mean?- how does it affect the graph?thanks 
RealiseNothing
what is that?It is Cowpea
Well for asymptotes, the graph will always tend towards it.Hi!i have a similar question to the question asked in this thread.how do you know what the graph looks like when you find out all the asymptotes, intercepts etc.?and what does 'symmetrical about the y and origin' mean?- how does it affect the graph?thanks

professorayton8
Member
- Joined
- Apr 28, 2012
- Messages
- 111
- Gender
- Female
- HSC
- 2013
so how would you graph y= 3x over x squared minus 4 ?
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
If you have questions, make your own thread.so how would you graph y= 3x over x squared minus 4 ?
Best not to hijack somebody else's. The social equivalent would be you asking the teacher a question, then me suddenly butting in and asking my own one.
professorayton8
Member
- Joined
- Apr 28, 2012
- Messages
- 111
- Gender
- Female
- HSC
- 2013
problem is... nobody is replying 
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Be patient, you will get an answer.problem is... nobody is replying
fishrushed
Member
- Joined
- Apr 20, 2012
- Messages
- 96
- Gender
- Male
- HSC
- 2013
i take it that u haven't learnt differentiation?so how would you graph y= 3x over x squared minus 4 ?