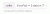8cos^2(x) = 2sin(x) +7
8(1-sin^2(x)) = 2sin(x) +7
8 -8sin^2(x) = 2sin(x) +7
Move everything to the RHS
8sin^2(x) +2sin(x) -1 =0
Two numbers that add to +2 and multiply to give (8 x -1) = -8
4 & -2
8sin^2(x) +4sin(x) -2sin(x) -1 =0
4sin(x) [ 2sin(x) +1] -(2sin(x) +1) =0
(2sin(x)+1) [ 4sin(x) -1] =0
Therefor
2sin(x) +1 =0 or 4sin(x) -1 =0
----
2sin(x) +1 =0 ---> sin(x) = -1/2
Related angle = sin^(-1) (1/2) = 30degrees
Sin is negative in 3rd and 4th quadrants
Therefore x= (180+30), (360-30) = 210, 330
--------------
4sin(x) -1 =0
sin(x) = 1/4
Related angle = sin^(-1) (1/4) = 14.4775.... degrees
Sin is positive in first and second quadrants
Therefore, x= 14.4775 , (180-14.4775) = 14.4775 , 165.5225 degrees
Changing to degrees and minutes
x= 14*29' , 165*31'
----
Therefore all solutions are x= 14*29' , 165*31' , 210*, 330*