Finding Domain is obvious for hyperbola, its pretty much what x can be, so what we are looking for is what x cant be.
For
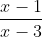
x cannot be 3.
Therefore our domain is all real x,

For Range however, in hyperbolas, what you can do is subsitute negative and positive infinity values into your calculator (sub in very large numbers), and see where they approach, for example in that above function, when you sub in values you will notice that you will get very close to 1,
our range is hence y is all real except y cannot equal to 1.
A useful tip, that will help you in 3U further curve sketching and finding range of hyperbolas is:
=\frac{mx-a}{nx-b} )
Our horizontal asymptote (and the value that y cannot be) is:

This works to find horizontal asympote for any function:
=\frac{ax^n+a_1 x^{n-1}+...}{bx^m+b_1 x^{m-1}+...} )
The rule is:
If n<.m, the horizontal asymptote is y=0
If n=m, horizontal asypmtote is y=a/b
If n>m, use polynomial division (do not worry about this right now)
That is just the logic behind it that is all.</m,>

