-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013 MX2 Marathon (archive) (1 Viewer)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
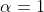 we get the Harmonic Series which
we get the Harmonic Series which  . You can construct the following bound to show this:
. You can construct the following bound to show this:

The RHS and so the result falls out.
and so the result falls out.
Now when we get
we get  and so for
and so for  we get
we get  \to \infty)
The second part is relatively simple to prove. When
The RHS
Now when
Last edited:
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
I feel sorry for your students.Let's light a fire here. No-one knows what school I teach at, right? But if you THINK I might be a teacher at your school, then there is a good chance some questions from this forum might be in your trial. Only 51 pages to sift through.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
 = \frac{\pi^2}{6})
so for we get
we get  = L) for some value L.
for some value L.
Now all I need is the case where , but I want to try do a more holistic proof rather than one by cases.
, but I want to try do a more holistic proof rather than one by cases.
so for
Now all I need is the case where
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
There is an easier method however.
You're first part is correct, for the second though, I'd advise against the case by case basis, it might work though.
so forwe get
for some value L.
Now all I need is the case where, but I want to try do a more holistic proof rather than one by cases.
There is an easier method however.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: HSC 2013 4U Marathon
Consider the curve y=1/x^p in the interval [1,infinity) and partition it into rectangles of unit sub-interval, and construct upper bound rectangles.
so forwe get
for some value L.
Now all I need is the case where, but I want to try do a more holistic proof rather than one by cases.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
 gives the inequality:
gives the inequality:

Consider the RHS, let where
where 


As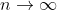




There may be an algebraic mistake somewhere as I haven't double checked my working, but it's the same idea nonetheless.
Constructing rectangle bounds for the curve
Consider the RHS, let
As
There may be an algebraic mistake somewhere as I haven't double checked my working, but it's the same idea nonetheless.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Yep that is pretty much it.Constructing rectangle bounds for the curvegives the inequality:
Consider the RHS, letwhere
As
There may be an algebraic mistake somewhere as I haven't double checked my working, but it's the same idea nonetheless.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
I don't see a need to but feel free to do so if it will help.Can students be expected to use the fundamental theorem of calculus freely?
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
For something like part i) of your most recent question, you would need to provide the students with a rigorous definition of integration from which to work ...as this is not assumed knowledge in 4U. You also need to state what kind of functions f you want this to be proven for.
(Unless by "prove" you mean "provide a heuristic argument for why this is true using the informal mx2 notion of an integral").
For something like part i) of your most recent question, you would need to provide the students with a rigorous definition of integration from which to work ...as this is not assumed knowledge in 4U. You also need to state what kind of functions f you want this to be proven for.
(Unless by "prove" you mean "provide a heuristic argument for why this is true using the informal mx2 notion of an integral").
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
) with width
with width 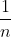
Just sum this from 1 to infinity to get the area under the curve.
The first part is taking infinite rectangles between the limits of 1 and 2. Their height will be
Just sum this from 1 to infinity to get the area under the curve.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Similar logic is there when deriving integrals for Volumes question, is this not rigorous/not in syllabus ?
I took the first part only from a STEP paper, it said 'Justify by means of a sketch', is using the word prove changing the meaning the original question had?
Is there a problem with the argument; that considering finite n, the sum of the lower rectangles of width 1/n is approximately the area (which is the integral), and then saying as n increases without bound the rectangles all sum up to become the area?For something like part i) of your most recent question, you would need to provide the students with a rigorous definition of integration from which to work ...as this is not assumed knowledge in 4U. You also need to state what kind of functions f you want this to be proven for.
(Unless by "prove" you mean "provide a heuristic argument for why this is true using the informal mx2 notion of an integral").
Similar logic is there when deriving integrals for Volumes question, is this not rigorous/not in syllabus ?
I took the first part only from a STEP paper, it said 'Justify by means of a sketch', is using the word prove changing the meaning the original question had?
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
1. What is the definition of area itself? (If you choose to define the integral via area).
2. How do you know that as n->inf the rectangles "area" approaches the "area" under the curve? Beyond the fact that the pictures look more and more alike.
3. You should state an assumption like continuity on f to guarantee those expressions make sense. If you don't assume something like this and your function is highly irregular, then the heuristic of measuring the "area" of things by rectangular approximations breaks down (and indeed the Riemann integral is not defined for such functions).
The main reason I am stressing these things is that typically, the integral is DEFINED via sums of the sort on the RHS, and "area under curves" is defined via this rigorous notion of integration. This puts things on a solid logical basis.
That's about as good as you can do with mx2 definitions and notions, but it is certainly not rigorous as the object you are proving things about (the Riemann integral) is not rigorously defined. Other things to think about:Is there a problem with the argument; that considering finite n, the sum of the lower rectangles of width 1/n is approximately the area (which is the integral), and then saying as n increases without bound the rectangles all sum up to become the area?
Similar logic is there when deriving integrals for Volumes question, is this not rigorous/not in syllabus ?
1. What is the definition of area itself? (If you choose to define the integral via area).
2. How do you know that as n->inf the rectangles "area" approaches the "area" under the curve? Beyond the fact that the pictures look more and more alike.
3. You should state an assumption like continuity on f to guarantee those expressions make sense. If you don't assume something like this and your function is highly irregular, then the heuristic of measuring the "area" of things by rectangular approximations breaks down (and indeed the Riemann integral is not defined for such functions).
The main reason I am stressing these things is that typically, the integral is DEFINED via sums of the sort on the RHS, and "area under curves" is defined via this rigorous notion of integration. This puts things on a solid logical basis.
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Second part is still open though.
Ah alright then :sThat's about as good as you can do with mx2 definitions and notions, but it is certainly not rigorous as the object you are proving things about (the Riemann integral) is not rigorously defined. Other things to think about:
1. What is the definition of area itself? (If you choose to define the integral via area).
2. How do you know that as n->inf the rectangles "area" approaches the "area" under the curve? Beyond the fact that the pictures look more and more alike.
3. You should state an assumption like continuity on f to guarantee those expressions make sense.
The main reason I am stressing these things is that typically, the integral is DEFINED via sums of the sort on the RHS, and "area under curves" is defined via this rigorous notion of integration. This puts things on a solid logical basis.
Second part is still open though.
- Status
- Not open for further replies.

