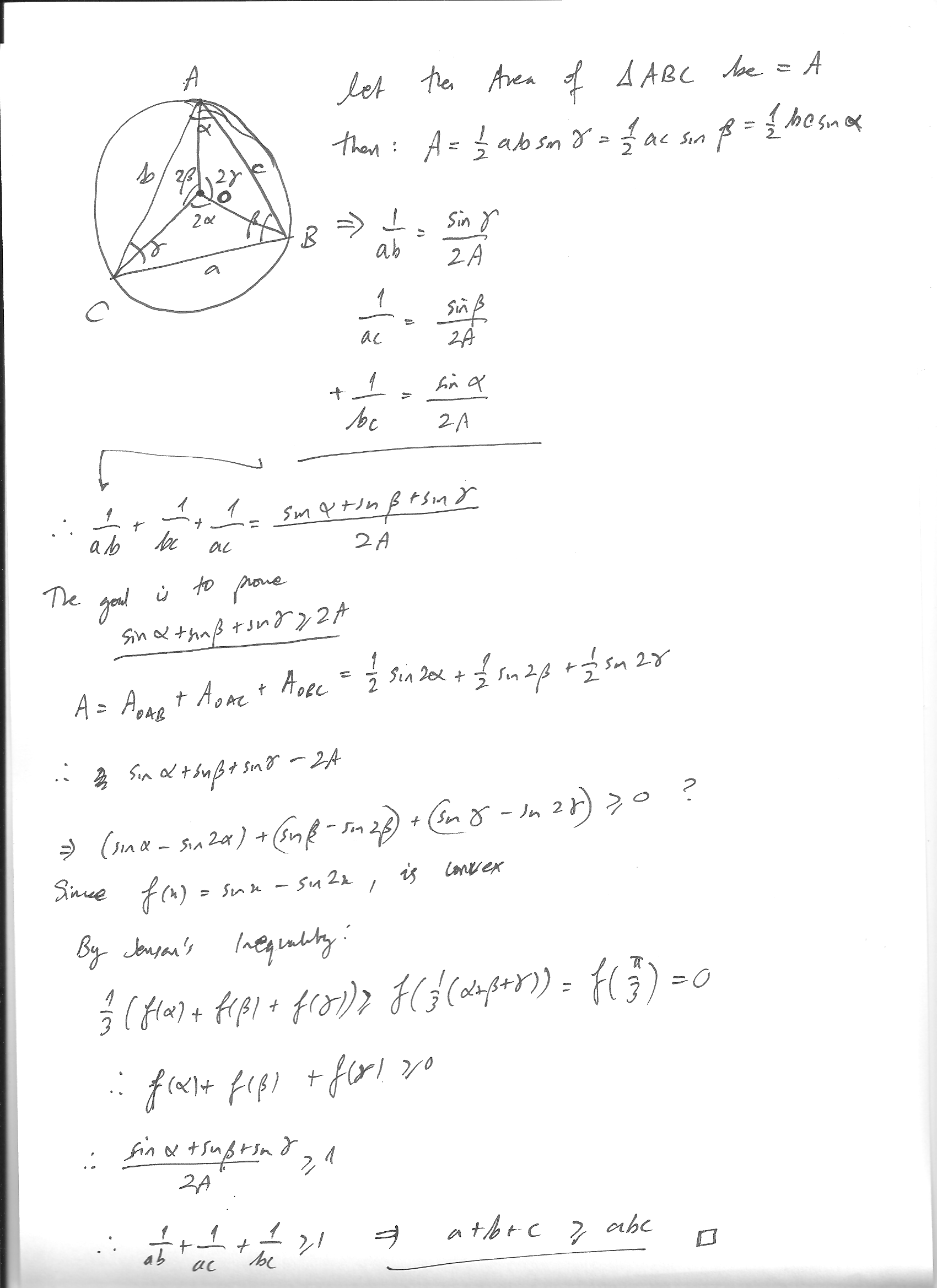Re: HSC 2014 4U Marathon - Advanced Level
Change x+1 to X and y+1 to Y,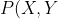=(X^2+(Y-2)^2)\cdot((X-2)^2+Y^2))
Symmetry is preserved.
Your counterexample is valid.
Why does your "rule" apply for the question Sy asked, but not for the expression in this post? Have to think about this question. Because the symmetry idea can only apply to cyclic expressions?
I have made a mistake in my last post.Because of the constants.
Change x+1 to X and y-1 to Y,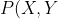=(X^2+Y^2)\cdot((X-2)^2+(Y+2)^2))
Change x+1 to X and y+1 to Y,
Symmetry is preserved.
Your counterexample is valid.
Why does your "rule" apply for the question Sy asked, but not for the expression in this post? Have to think about this question. Because the symmetry idea can only apply to cyclic expressions?